Setup
Para asegurarnos de que el siguiente análisis sea reproducible se utilizará la siguiente librería:
library(tidyverse)
Los datos y la estructura general han sido tomados del libro “An Introduction to Statistical Learning”, el cual se puede encontrar aquí.
Cargando los datos:
data = readr::read_csv("https://www.statlearning.com/s/Advertising.csv")
data = data[,-1]
Motivación
Supongamos que ha sido contratado en una empresa como Científico de Datos y le piden que investigue la relación entre los gastos en marketing y las ventas de 200 productos:
| Id | TV | radio | newspaper | sales |
|---|---|---|---|---|
| 1 | 230.1 | 37.8 | 69.2 | 22.1 |
| 2 | 44.5 | 39.3 | 45.1 | 10.4 |
| 3 | 17.2 | 45.9 | 69.3 | 9.3 |
| 4 | 151.5 | 41.3 | 58.5 | 18.5 |
| 5 | 180.8 | 10.8 | 58.4 | 12.9 |
Donde cada celda de las columnas $TV$, $radio$, $newspaper$ representa el gasto en publicidad en miles de USD y $sales$ representa el volumen de ventas en un mercado particular.
En este contexto, la variable $sales$ representa nuestra variable objetivo o variable de salida, output variable o target y $TV$, $radio$ y $newspaper$ son las variables de entrada, input variables o predictores.
¿Qué relación tiene $sales$ con cada uno de los predictores?
data %>%
pivot_longer(!sales, names_to="canal",values_to = "expend")%>%
ggplot(aes(x=expend,y=sales))+
geom_point()+
facet_wrap(~canal,scales = "free_x")+
theme_bw()+
labs(title = "Relación entre el gasto en publicidad y las ventas por canal",
x = "\n Gasto en publicidad (miles de USD)",
y = "Ventas (miles de unidades)\n")
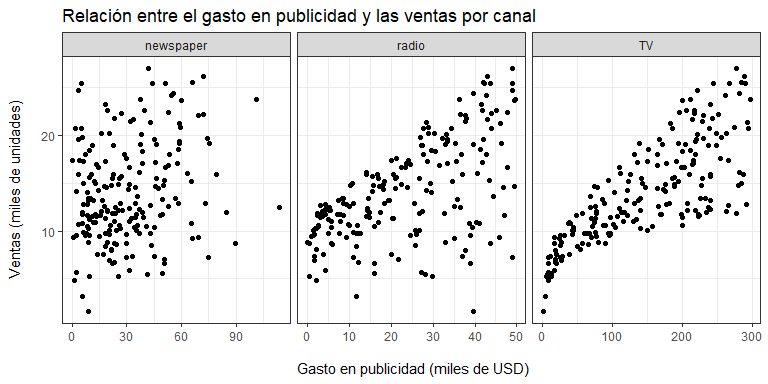
Nótese que, invariablemente, a medida que se incrementa el gasto en publicidad, las ventas también se incrementan. Ahora, si esta relación fuera estable, podría ser aproximada a través de una línea. Por ejemplo:
data %>%
pivot_longer(!sales, names_to="canal",values_to = "expend")%>%
ggplot(aes(x=expend,y=sales))+
geom_point()+
facet_wrap(~canal,scales = "free_x")+
theme_bw()+
geom_smooth(formula = y ~ x,method = "lm",se=F)+
labs(title = "Relación entre el gasto en publicidad y las ventas por canal",
x = "\n Gasto en publicidad (miles de USD)",
y = "Ventas (miles de unidades)\n")
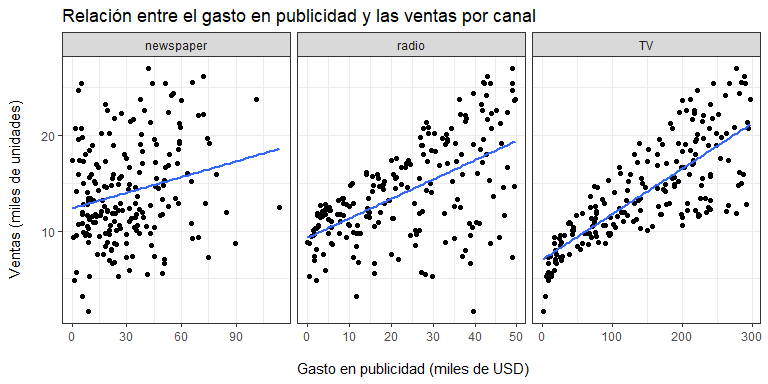
La pregunta es, ¿por qué una línea? Nótese que saber que se vendieron $22.1$ mil unidades del producto 1 y $10.4$ mil del producto 2 mientras que para el primero se invirtieron USD $69.2$ mil en publicidad por periódicos y para el segundo USD $45.1$ mil, no nos dice absolutamente nada. Son datos aislados.
Pero, ¿qué tal si pudiéramos explotar la relación que existe entre las ventas y el gasto para predecir (anticiparnos, aproximar) las ventas esperadas en base a la información que tenemos de todos los productos? Esto es justamente lo que esta aproximación lineal pretende lograr. Sin embargo, no estamos limitados a una relación estrictamente lineal:
data %>%
pivot_longer(!sales, names_to="canal",values_to = "expend")%>%
ggplot(aes(x=expend,y=sales))+
geom_point()+
facet_wrap(~canal,scales = "free_x")+
theme_bw()+
geom_smooth(formula = y ~ x+I(x^2),method = "lm",se=F)+
labs(title = "Relación entre el gasto en publicidad y las ventas por canal",
x = "\n Gasto en publicidad (miles de USD)",
y = "Ventas (miles de unidades)\n")
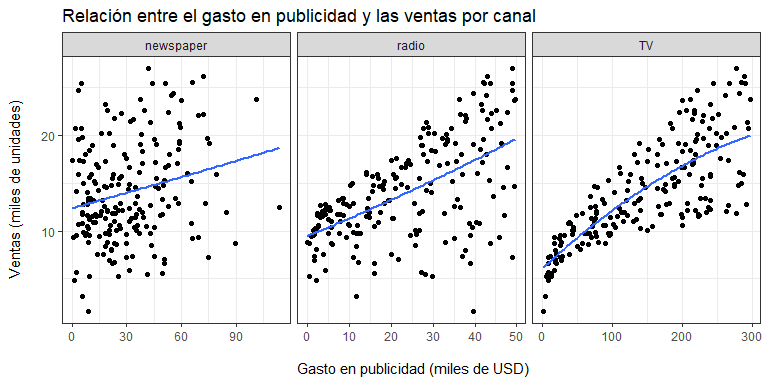
En este caso, la relación entre gasto en publicidad en $TV$ respecto a las ventas, $sales$, sugiere una relación no lineal
El mismo problema en 3D
Para ganar un poco de intuición, a veces es interesante plantearse el problema en 3 dimensiones.
De forma general, imagine que se tiene el siguiente proceso generador de datos: $X \sim N(0,1)$, $Z\sim N(0,1)$ y $Y = X + Z - X^{2} - Z^{2}$.
Este puede ser representado geométricamente como:
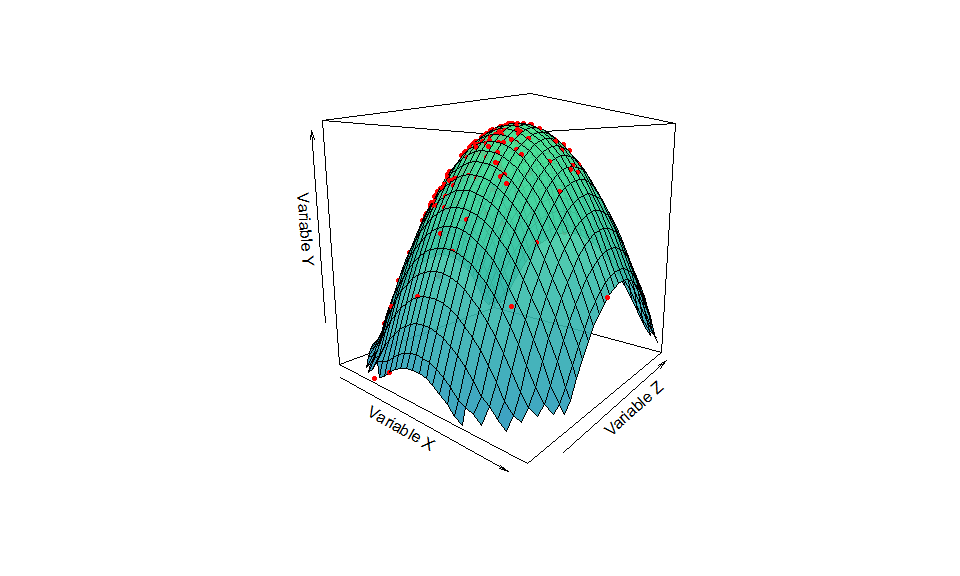
Este PGD es intrínsecamente no lineal y lo sabemos porque lo hemos simulado. En la práctica no lo conocemos, pero tratamos de aproximarlo utilizando la teoría, el juicio experto y el análisis de datos.
Una aproximación lineal nos puede dar un ajuste bueno “en promedio”:
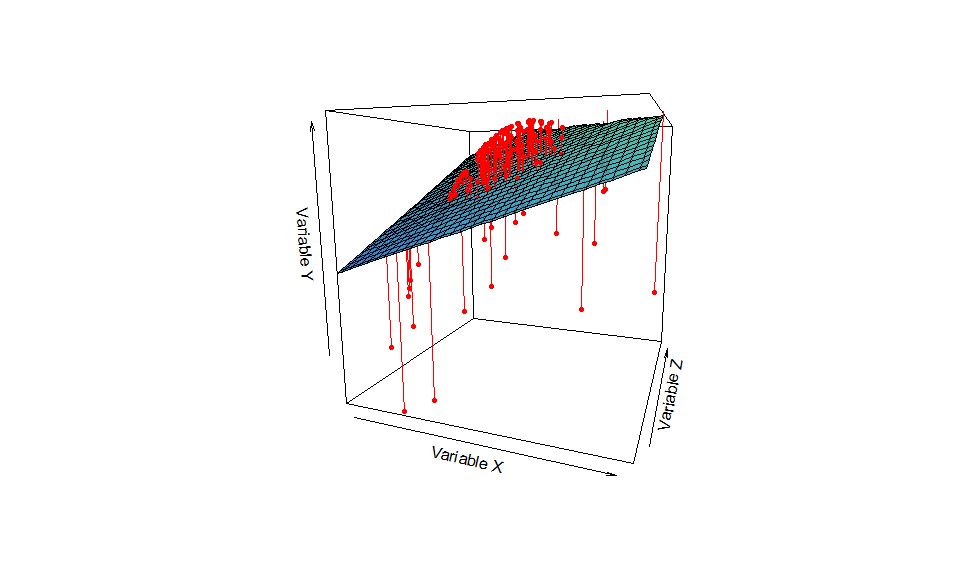
Nótese que se ajusta un “hiperplano” que no coincide exactamente con los puntos. Nótese que en una aplicación específica, el analista no conoce realmente el proceso que dio origen a los datos y, armado con sus conocimientos matemáticos, estadísticos e institucionales (juicio experto) trata de replicar el mismo.
En el caso de los datos revisados anteriormente, una aproximación lineal se vería como:
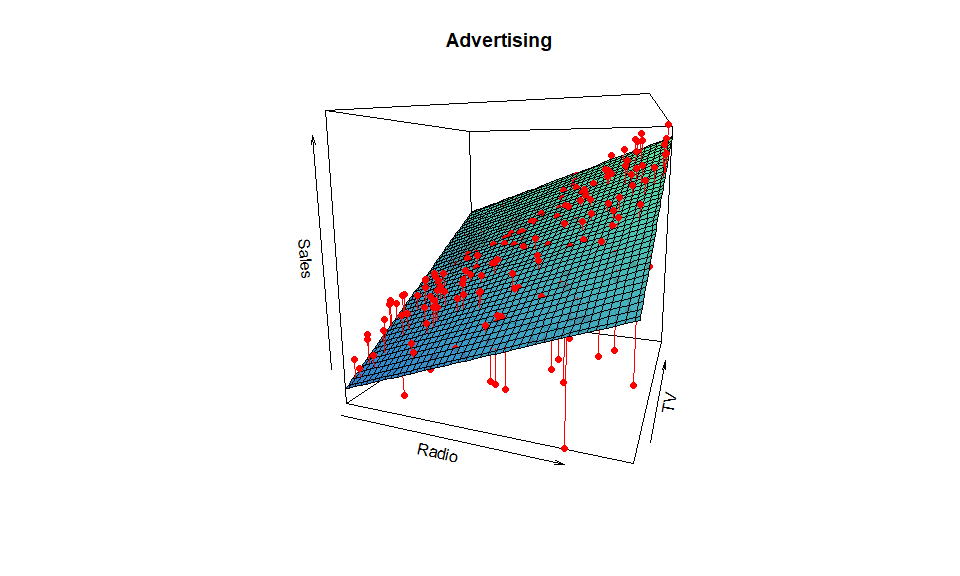
El cual parece replicar los datos, al menos en un sentido “promedio”.
Planteamiento general
Suponga que observamos una determinada cantidad $Y$ y $p$ diferentes predictores, $X_1,X_2,…,X_p$. Asumiendo que existe una relación entre $Y$ y $\mathbf{X} =X_1,X_2,…,X_p$ se puede escribir compactamente como:
$$Y = \mathcal{f}(\mathbf{X})+e$$
Donde $\mathcal{f}$ es una función concreta pero desconocida de $X_1,X_2,…,X_p$ y $e$ es un término de error aleatorio, que es independiente de $X$ y en, en promedio, es igual a $0$.
En esta formulación $\mathcal{f}$ representa la información sistemática que se puede extraer de $Y$ observando $\mathbf{X}$.
Ahora, Como la función $\mathcal{f}$ es desconocida uno de los primeros trabajos es estimarla a partir de los datos. Cuando se habla de una estimación, usualmente se coloca un “sombrero” para distinguirla de su valor real y desconocido. Por ejemplo, podríamos hablar de $\mathcal{\hat{f}}(\mathbf{X})$ como una estimación de $\mathcal{f}(\mathbf{X})$ y $\hat{Y}$ (“Y sombrero”) como una estimación de $Y$.
En este sentido, estamos ante un problema de naturaleza estadística: ¿cómo puedo inferir una relación entre variables cuando solo tengo una parte de la información?
En esencia, el aprendizaje estadístico, tal cual como lo definen Gareth et al (2021), se refiere al conjunto de métodos y aproximaciones para estimar $\mathcal{f}$ de una forma “razonable”.
¿Para qué estimar $\mathcal{f}$?
Hay, quizás, $3$ razones y/o aplicaciones por las cuales uno quisiera estimar $\mathcal{f}$:
- Predicción
- Inferencia
- Inferencia causal
Sin embargo, dependiendo del uso de esta relación, se deberán verificar ciertas condiciones sobre $\mathcal{f}$.
Predicción
En muchas situaciones, un conjunto de variables o insumos $\mathbf{X}$ están disponibles y tienen información relevante y relacionada con $Y$ pero ésta última es desconocida o es difícil de obtener. Por ejemplo:
- Dados las características y perfil de un cliente y su historial crediticio, ¿cuál es la probabilidad de que devuelva un préstamo?
- Dado el historial de búsqueda y likes de un individuo en facebook, ¿cuál es la probabilidad de que le interese un determinado producto?
- Dada las condiciones climáticas (temperatura), el número de incendios en el país y el costo de los insumos nos interesa saber el precio de la soya la próxima temporada.
- Dado el tipo de canciones que escuchan los usuarios en Spotify, la cantidad de búsquedas relacionadas a “crisis financieras” en google y el número de veces que aparecen las palabras “crisis” o “recesión” en la prensa escrita, ¿cuánto es el crecimiento de la economía (PIB) el día de hoy?
En este contexto $\mathcal{f}$ puede tratada como una caja negra (o black box) pues no nos interesa la forma específica que tome siempre y cuando las predicciones para $Y$ sean acertadas. Es decir, se evalúa nuestra aproximación en base a los resultados.
Visto de otra forma, estimar implica, dada cierta información, calcular u aproximar un valor desconocido.
Nótese que la capacidad de $\mathcal{\hat{f}}$ para replicar $\mathcal{f}$ y, por tanto, de $\hat Y$ depende de dos cantidades: una sistemática y otra aleatoria. Recordando: $$Y = \underbrace{\mathcal{f}(\mathbf{X})}{sistemático} + \underbrace{e}{aleatorio} $$
Nosotros podemos trabajar sobre $\mathcal{f}(\mathbf{X})$ utilizando mejores técnicas para modelar la relación y tener mejores predicciones, $\hat Y$. Sin embargo, aún cuando $\mathcal{\hat{f}}(\mathbf{X}) \xrightarrow{p} \mathcal{f}(\mathbf{X})$, $\hat Y \ne Y$ debido a la naturaleza de $e$, que no puede ser reducido o eliminado.
Inferencia
Otras veces, uno puede estar interesando en entender la asociación entre $Y$ y las variables explicativas $X_1, X_2,…,X_p$.
En este contexto quisiéramos estimar $\mathcal{f}(\mathbf{X})$ pero nuestro objetivo no es obtener buenos valores de $\hat Y$, sino encontrar la forma de $\mathcal{f}(\mathbf{X})$ que más se asemeje a la realidad.
Este problema se suele describir como entender el proceso generador de datos. Preguntas asociadas al uso de datos para realizar inferencia son:
- ¿Qué predictores/variables explicativas están asociadas con la respuesta o variable $Y$?
- ¿Qué relación tiene $Y$ con cada variable explicativa?
- ¿Puede aproximarse $Y = \mathcal{f}(\mathbf{X})$ como una relación lineal o $f(\mathbf{X})$ tiene una estructura más compleja?
En el caso del ejemplo que se dio previamente, (la relación entre las ventas de cada producto y la inversión en los distintos canales de publicidad), uno podría necesitar la respuesta a las siguientes preguntas para tomar decisiones:
- ¿Qué tipo de publicidad está asociado con las ventas?
- ¿Qué tipo de publicidad genera el mayor incremento en las ventas?
- ¿Cuánto más ventas tendríamos si incrementamos en USD 1 mil el gasto en publicidad en TV?
En este tipo de inferencia nos referimos al grado de asociación que existe entre la variable $Y$ y las variables explicativas, $\mathbf{X}$.
Inferencia causal
Todavía existe un tipo de inferencia más complejo que tiene que ver con la inferencia causal. En este caso, nos interesa el resultado a preguntas contrafactuales, es decir, situaciones que no han ocurrido.
Por ejemplo, si se da un bono anual a los estudiantes para no abandonar el colegio, ¿cuántos individuos no lo dejarán? O, si se desea entender el impacto que tiene un programa de licenciatura sobre el salario de un individuo, ¿cómo podemos obtener conclusiones?
El tipo de inferencia causal ha sido estudiado ampliamente en el contexto de la econometría por los economistas y cientistas sociales y los supuestos bajo los cuales se pueden obtener los resultados son diferentes a los utilizados en el contexto del aprendizaje estadístico, aprendizaje automático y/o machine learning.
Aún cuando existen métodos comunes en las diferentes disciplinas, como el uso del análisis de regresión, la econometría se enfoca principalmente en el diseño experimental y la estructura de los datos. Es decir, no se pueden responder preguntas del tipo causal con cualquier conjunto de datos.
Se podría decir que el problema principal que enfrenta el analista es el sesgo de selección que en el contexto del análisis de regresión recibe el nombre de sesgo de variables omitidas.
Un buen libro introductorio a los métodos econométricos (state-of-the-art) es el de Scott Cunningham que puede encontrarse online aquí.
Nota: En lo que resta el análisis se enfocará en el problema de la predicción únicamente.
¿Cómo estimar $\mathcal{f}$?
Se pueden clasificar los métodos para obtener $\mathcal{f}(\mathbf{X})$ en las siguientes categorías:
- Métodos paramétricos
- Métodos no paramétricos
O, adicionalmente:
- Modelos lineales
- Modelos no lineales
El objetivo general es aplicar un método de aprendizaje estadístico que nos ayude a obtener la función desconocida $\mathcal{f}(\mathbf{X})$. Es decir, buscamos una función $\hat{f}$ tal que $Y \approx \hat{f}(X)$ para cualquier observación de $(X,Y)$.
Métodos paramétricos
Los métodos paramétricos implican un proceso en dos etapas:
- Realizar un supuesto sobre la forma funcional de $\mathcal{f}$. Por ejemplo, si $\mathcal{f}$ fuera lineal en $\mathbf{X}$: $$f(\mathbf{X}) = \beta_0 + \beta_1X_1 + \beta_2X_2+…+\beta_pX_p$$
- Una vez que el modelo se ha seleccionado, se necesita un procedimiento matemático que utilice los datos para estimar o ajustar el modelo.
En el caso del paso 1, el hecho de realizar un supuesto de linealidad, reduce o simplifica la modelación, pues solo debemos encontrar el valor de los $p+1$ parámetros $\beta_j ; \forall ; j=0, 1,2,3…,p$.
En cuanto al paso 2, existen varios métodos matemáticos para estimar los parámetros, por ejemplo, mínimos cuadrados ordinarios, máxima verosimilitud, método de momentos y distintos algoritmos cuando el modelo no tiene una solución cerrada o sea costosa computacionalmente (por ejemplo, es posible utilizar un algoritmo de optimización tal como gradient descent.
Como ventaja, los métodos paramétricos son más fáciles de estimar o entrenar pero, como desventaja, el modelo que usemos puede simplificar demasiado la verdadera forma de $\mathcal{f}$ y, por tanto, nuestra estimación, $\hat Y$, será pobre.
Una forma de reducir este problema es elegir formas funcionales más complejas aunque esto no es gratis pues agregar complejidad puede conducir a un problema conocido como sobreajuste ( overfitting ) a los datos, lo cual implica que el modelo no solo aprende los patrones sistemáticos de los datos sino también los errores o el ruido que existe.
Una lista de modelos paramétricos:
- Regresión lineal
- Regresión logística
- Análisis Discriminante Lineal
- Perceptron
- Naive Bayes
- Red neuronal simple
Modelos no paramétricos
Estos modelos no hacen un supuesto explícito sobre la forma funcional de $\mathcal{f}$ y ajustan funciones más precisas respecto a los datos.
La desventaja es que, para que estos modelos funcionen, necesitan una mayor cantidad de datos para realizar un buen ajuste.
Una lista de estos métodos:
- k-Nearest Neighbors
- Árboles de decisión (como CART o C4.5)
- Support Vector Machines
Evaluación de un modelo estadístico
Bondad de ajuste: Regresión
Finalmente, como el problema trata de la predicción, se debe conceptualizar cómo se cuantifica el grado en el cual una observación está cerca del valor predicho para esa observación.
Una medida común utilizada en problemas donde la variable $Y$ es numérica (problemas de regresión) es el Error medio al cuadrado o Mean Square Error (MSE): $$MSE = \frac{1}{n}\displaystyle\sum_{i=1}^{n}\big(y_i-\hat y_i\big)^2 $$
donde $\hat y_i$ es una predicción particular de un vector $\hat Y$ para el individuo $i$. En el caso de un modelo lineal:
$$ \hat y_i = \hat\beta_0 + \hat\beta_1x_{1i}+\hat\beta_2x_{2i}+…+\hat\beta_px_{pi} \quad \forall i = 1,2,…,n $$
Claramente, si $\hat Y$ está cerca de $Y$, el $MSE$ será pequeño.
La fórmula del $MSE$ mostrada anteriormente asume que se ha calculado con todo el conjunto de datos. Es decir, utilizamos todos los datos para entrenar el modelo. A estos datos se los conoce como datos de entrenamiento o training data.
Como lo que nos interesa es utilizar el modelo para hacer predicciones sobre datos diferentes a los datos con los que el modelo ha sido entrenado, debemos calcular el $MSE$ con un conjunto de datos de prueba o test data.
Bondad de Ajuste: Clasificación
En el contexto de la clasificación, se busca estimar también $\mathcal{f}$ sobre la base del conjunto de entrenamiento, ${(x_1,y_1), (x_2,y_2),…,(x_n,y_n)}$ solo que ahora $y_1, y_2,…,y_n$ son variables cualitativas las que, usualmente, toman solamente dos valores: $0$ y $1$.
La forma más común de medir la precisión de nuestro estimado $ \mathcal{\hat f}$ es mediante la tasa de error (o error rate), la cual puede ser calculada tanto sobre los datos de entrenamiento como con los datos de prueba: $$ER = \displaystyle\frac{1}{n} \displaystyle\sum_{i=1}^{n}I(y_i \ne \hat y_i) $$
donde $\hat y_i$ es la categoría predicha para la observación $i$ usando $\hat f$ e $I(y_i \ne \hat y_i)$ es una variable indicador que toma el valor de $1$ si $y_i \ne \hat y_i$ (si el valor predicho es distinto al valor realizado, es decir, si se detecta un error) y $0$ si $y_i = \hat y_i$.
Finalmente, existen varias formas de mirar a $ER$ y cuando se avancen modelos de clasificación se construirá una matriz de confusión la cual resulta más atractiva analíticamente.
Apéndice matemático: La ecuación que pasa por dos puntos
Se debe recordar que la ecuación de la línea es: $$ y = a + bx$$
Esta ecuación describe cualquier línea, dado los valores $a$ y $b$.
Matemáticamente, dado dos puntos es posible ajustar una línea que pase por ambos: $$y-y_1 = \frac{y_2-y_1}{x_2-x_1}(x-x_1)$$ Por ejemplo, imagine los dos pares ordenados de la forma $(x_i, y_i)$: $(1,2)$ y $(7,6)$
$$ \begin{aligned} y-2 &= \frac{6-2}{7-1}(x-1) \\ y &= \frac{2}{3}x - \frac{2}{3} + 2 \\ y &= \frac{4}{3} + \frac{2}{3}x \end{aligned} $$
Gráficamente:
ggplot(data.frame(x=c(1,7),y=c(2,6)), aes(x,y))+
xlim(c(0,10))+
ylim(c(0,10))+
geom_abline(intercept = 4/3, slope=2/3, color="blue")+
geom_point(size=2.5)+
theme_bw()+
annotate("text", x =4, y=5, label="y == frac(4,3) + frac(2,3)*x", parse=T)
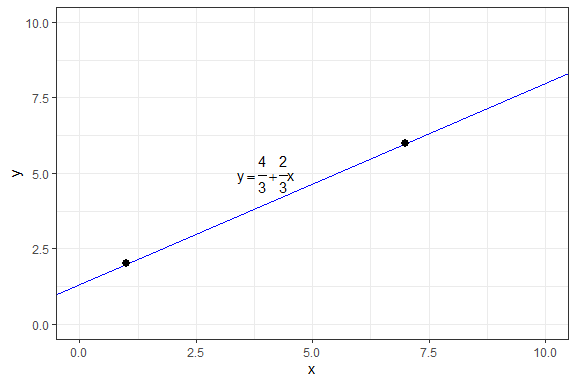
De esta línea sabemos que, cuando $x$ se incrementa en una unidad, $y$ se incrementa en $\frac{2}{3}$. Ahora, si $x$ fuera el gasto en publicidad y $y$ las ventas, esta relación podría ser explotada para beneficio de la empresa. La cuestión, sin embargo, es cómo obtenemos $a$ y $b$ cuando hay más de dos puntos.
Finalmente, si no estuviéramos satisfechos con el tipo de ajuste que se ha realizado (lineal) podríamos también (siempre que podamos inferir los parámetros) realizar un ajuste cuadrático del tipo: $$y= a+bx+cx^2$$
¿Qué diferencia tiene respecto a la relación lineal? En particular, la interpretación de la tasa de cambio o derivada.
$$\frac{dy}{dx} = b+2cx $$
Es decir, dependiendo del valor de $x$ el efecto podría ser uno u otro.