Introducción
El presente documento tiene como objetivo servir como material de apoyo a lo revisado en clases.
En primer lugar, se replicará el ejercicio elaborado en clase utilizando R, tanto de forma rudimentaria (calculando las fórmulas) como de forma automática (utilizando alguna función).
En la segunda parte se introduce la librería wooldridge que habilita al estudiante a replicar los resultados del manual de econometría.
Replicando en R
Cargar datos
En esta parte vamos a reproducir el ejercicio realizado en clases. Para esto, lo primero que vamos a hacer es recrear el conjunto de datos. Se utilizará la estructura conocida como data frame para almacenar la información.
datos <- data.frame(gpa = c(2.8, 3.4, 3, 3.5, 3.6, 3, 2.7, 3.7),
act = c(21, 24, 26, 27, 29, 25, 25, 30))
datos
| gpa | act |
|---|---|
| 2.8 | 21 |
| 3.4 | 24 |
| 3.0 | 26 |
| 3.5 | 27 |
| 3.6 | 29 |
| 3.0 | 25 |
| 2.7 | 25 |
| 3.7 | 30 |
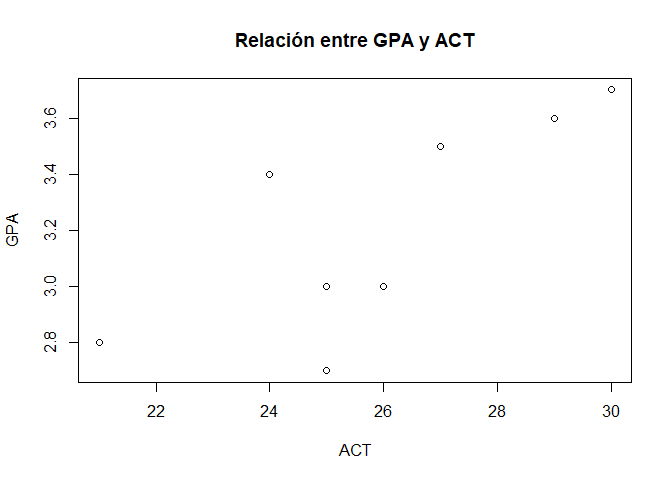
Dibujar los datos
Una forma interesante para conocer los datos es dibujándolos. Para ello vamos a utilizar la función nativa de $R$ conocida como plot():
plot(x= datos$act, y = datos$gpa,
main = "Relación entre GPA y ACT",
xlab = "ACT",
ylab = "GPA")
Estadísticos resumen
Nos puede interesar entender los principales indicadores de $gpa$, para eso podemos utilizar la función summary()
summary(datos$gpa)
Min. 1st Qu. Median Mean 3rd Qu. Max.
2.700 2.950 3.200 3.212 3.525 3.700
Esta función nos da una idea rápida de los principales momentos de la distribución.
Regresión
El modelo que deseamos estimar es el siguiente:
$$GPA = \beta_0 + \beta_1ACT+u$$
Implementación manual
Lo primero que vamos a calcular son los estimados para los betas, $ \hat\beta_0$ y $\hat\beta_1$ a partir de las fórmulas obtenidas aplicando los Mínimos Cuadrados Ordinarios, es decir:
$$\hat\beta_{1}^{MCO} = \frac{Cov(X,Y)}{Var(X)}$$
beta1 <- cov(datos$gpa, datos$act)/var(datos$act)
beta1
[1] 0.1021978
$$\hat\beta_{0}^{MCO} = \bar{Y} - \hat\beta_{1}^{MCO}\bar{X} $$
beta0 <- mean(datos$gpa)- beta1*mean(datos$act)
beta0
[1] 0.5681319
Ahora, para estimar el error estándar de cada estimador bajo el supuesto de homocedasticidad:
$$\begin{aligned} ee\big(\hat\beta_{1}^{MCO}\big) &= \sqrt{\frac{\hat\sigma^{2}_{u}}{ \sum_{i=1}^{n}(X_{i}-\bar{X})^2}} \end{aligned}$$
$$\begin{aligned} ee\big(\hat\beta_{0}^{MCO}\big) &= \sqrt{\frac{\hat\sigma^{2}_{u}\sum_{i=1}^{n}X_{i}^{2}}{n\sum_{i=1}^{n}(X_{i}-\bar{X})^{2}}} \end{aligned}$$
Adicionalmente, la varianza de la regresión:
$$\hat{\sigma}^{2}_{u}=\frac{\sum_{i=1}^{n}\hat{u}_{i}^{2}}{n-k} $$
donde $n$ es el número de observaciones y $k$ el número de parámetros a ser estimados.
Estimando la varianza y el error estándar de la regresión:
gpa_hat = beta0+beta1*datos$act
residuos = datos$gpa - gpa_hat
var_u = sum(residuos^2)/(length(residuos)-2)
var_u
[1] 0.07245421
ee_u <- sqrt(var_u)
ee_u
[1] 0.2691732
Estimando el error estándar de $\hat\beta_{1}^{MCO}$
ee_beta1 = sqrt(var_u/sum((datos$act-mean(datos$act))^2))
ee_beta1
[1] 0.03569202
Estimando el error estándar de $\hat\beta_{0}^{MCO}$
ee_beta0 = sqrt((var_u*sum(datos$act^2))/(length(datos$act)*sum((datos$act-mean(datos$act))^2)))
ee_beta0
[1] 0.9284214
Ahora se estiman los estadísticos $t_0$ y $t_1$:
t0 <- abs(beta0/ee_beta0)
t0
[1] 0.6119332
t1 <- abs(beta1/ee_beta1)
t1
[1] 2.863324
Finalmente, se calcula el $R^2$:
$$R^{2} = 1 - \frac{\sum_{i=1}^{n}\hat{u_{i}}^{2}}{ \sum_{i=1}^{n}({Y_{i}}-\bar{Y})^{2}}$$
R2 <- 1 - (sum(residuos^2)/sum((datos$gpa-mean(datos$gpa))^2))
R2
[1] 0.5774238
Coleccionando los resultados:
| Variable | Valor |
|---|---|
| $\hat\beta_{0}^{MCO}$ | $0.59$ |
| $\hat\beta_{1}^{MCO}$ | $0.10$ |
| $ee\big(\hat\beta_{0}^{MCO}\big)$ | $0.93$ |
| $ee\big(\hat\beta_{1}^{MCO}\big)$ | $0.04$ |
| $\hat\sigma_{u}$ | $0.27$ |
| $t_0$ | $0.61$ |
| $t_1$ | $2.86$ |
| $R^2$ | $0.57$ |
Implementación en R
La forma en que en R se estima el modelo de regresión es mediante la función lm() (en inglés, linear models) y, en general, se especifica como lm(y ~ x, data):
mco <- lm(gpa ~ act, data= datos)
modelsummary::modelsummary(list("MCO"=mco),
gof_map = c("nobs", "r.squared"),
estimate = "{estimate}{stars}",
output="markdown" )
| MCO | |
|---|---|
| (Intercept) | 0.568 |
| (0.928) | |
| act | 0.102* |
| (0.036) | |
| Num.Obs. | 8 |
| R2 | 0.577 |
Así, en la notación vista en clase, la recta estimada es:
$$\widehat{GPA} = \underset{(0.93)}{0.57}+\underset{(0.04)}{0.10}ACT $$
¿Cómo se interpreta? Básicamente, el modelo captura que, por cada incremento en $1$ punto del $ACT$ el $GPA$ se incrementa en $0.10$ unidades.
Ejercicio de Wooldridge
En esta parte se va a utilizar el conjunto de datos wage1 que acompaña el libro de Wooldridge. El detalle de los datos se puede encontrar aquí.
Setup
Lo primero que se debe hacer es instalar las librerías que se van a ocupar. En este caso necesitamos la librería de wooldridge para utilizar los datos que acompañan al manual.
install.packages("wooldridge")
Una vez instalada, se debe utilizar la función library() para activarla en la sesión actual:
library(wooldridge)
Una vez ejecutado el código anterior, tenemos disponibles todos los datos del manual de econometría. Por tanto, vamos a cargar los datos de wage1.
data("wage1", package = "wooldridge")
Una vez que los datos están cargados, una forma de verlos es haciendo click en el objeto (data frame) llamado wage1 que se muestra en el global enviroment. Otra forma es escribir en la consola el código View(wage1) para abrir el visualizador de datos.
head(wage1)
| wage | educ | exper | tenure | nonwhite | female | married | numdep | smsa | northcen | south | west | construc | ndurman | trcommpu | trade | services | profserv | profocc | clerocc | servocc | lwage | expersq | tenursq |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 3.10 | 11 | 2 | 0 | 0 | 1 | 0 | 2 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1.131402 | 4 | 0 |
| 3.24 | 12 | 22 | 2 | 0 | 1 | 1 | 3 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1.175573 | 484 | 4 |
| 3.00 | 11 | 2 | 0 | 0 | 0 | 0 | 2 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1.098612 | 4 | 0 |
| 6.00 | 8 | 44 | 28 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1.791759 | 1936 | 784 |
| 5.30 | 12 | 7 | 2 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1.667707 | 49 | 4 |
| 8.75 | 16 | 9 | 8 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 2.169054 | 81 | 64 |
Algo que llama la atención de los datos es que hay muchos codificados con $0$ y $1$. A estas variables se las conoce como dummies. Para mayor información se puede utilizar la ayuda de lenguaje ?wage1 en la consola.
Análisis de información
En este caso, la variables que nos interesan son wage y educ, puesto que nos importa estimar la relación que existe entre $1$ año más de educación y los salarios.
Inicialmente podemos ver cómo se distribuyen estas variables utilizando la función hist()
hist(wage1$wage)
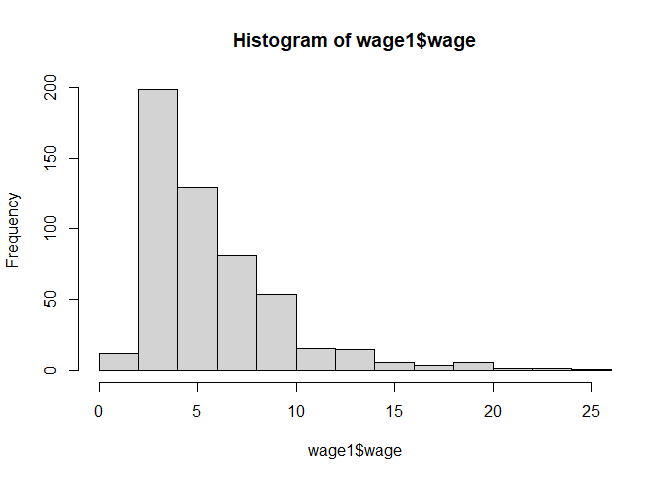
El gráfico que obtenemos de la función hist() es bastante sencillo y nos permite entender de forma rápida cómo se distribuye la variable en nuestro conjunto de datos.
Si quisiéramos elaborar un poco más el gráfico para presentarlo, podemos darle más información pasando más parámetros:
hist(wage1$wage,
xlab = "Salario por hora (USD)",
ylab = "Frecuencia",
main = "Histograma del salario por hora",
col = "steelblue")
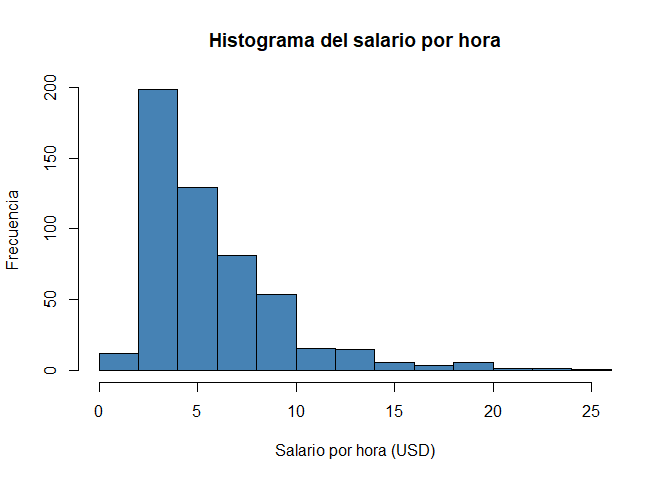
En este caso se añadieron los títulos de los ejes, xlab y ylab, el título principal main y algo de color, col. El detalle de los parámetros se puede ver escribiendo ?hist en la consola.
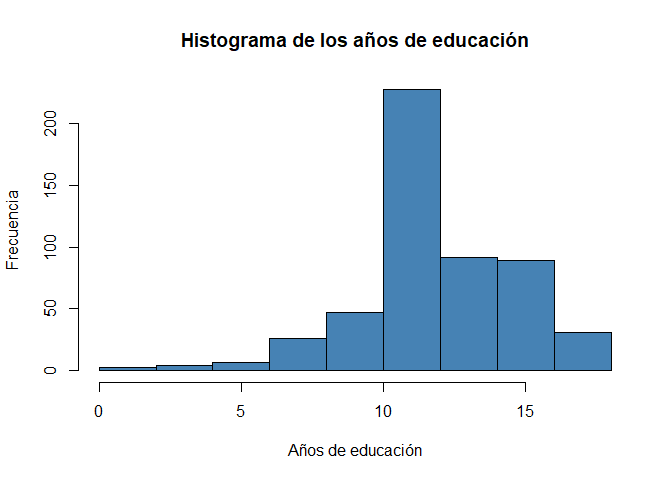
Podemos escribir el mismo código pero, esta vez, para la variable educ:
hist(wage1$educ,
xlab = "Años de educación",
ylab = "Frecuencia",
main = "Histograma de los años de educación",
col = "steelblue")
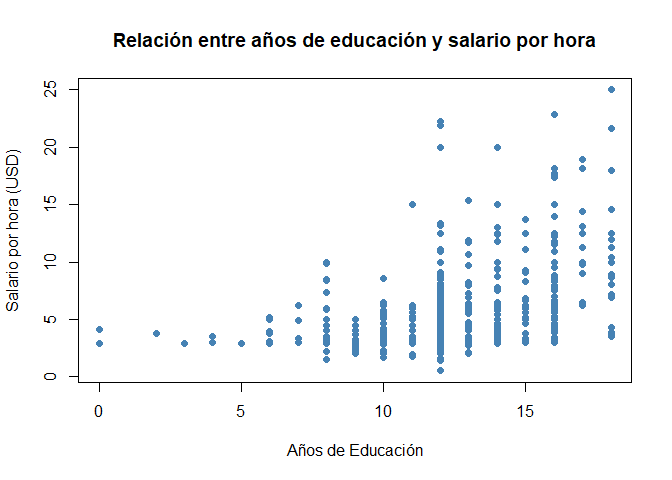
Otra cosa interesante es entender gráficamente la relación entre los años de educación y el salario por hora. Eso se puede lograr mediante una diagrama de dispersión.
En R se puede implementar con la función plot():
plot(x=wage1$educ, y=wage1$wage,
main = "Relación entre años de educación y salario por hora",
xlab = "Años de Educación",
ylab = "Salario por hora (USD)",
col = "steelblue",
pch = 19)
Regresión
El objetivo del ejercicio era entender si existe una relación entre los salarios, wage y los años de educación, educ. Para esto podemos utilizar el análisis de regresión.
Vamos a plantear el siguiente modelo poblacional:
$$Salarios = \beta_0 + \beta_1Educación + u$$
Esta relación podemos estimarla utilizando la función lm()
mco2 <- lm(wage ~ educ, data = wage1)
modelsummary::modelsummary(list("MCO"=mco2),
gof_map = c("nobs", "r.squared"),
estimate = "{estimate}{stars}",
output="markdown" )
| MCO | |
|---|---|
| (Intercept) | -0.905 |
| (0.685) | |
| educ | 0.541*** |
| (0.053) | |
| Num.Obs. | 526 |
| R2 | 0.165 |
Lo que se ha encontrado es lo siguiente:
$$\widehat{Salario} = \underset{(0.68)}{-0.90} + \underset{(0.05)}{0.54}Educación $$
Interpretación: Por cada año adicional de educación, en promedio, el salario se incrementa en $0.54$ dólares por hora.
Nótese que solamente $Educación$ es estadísticamente significativa al $1\%$.
Conclusiones
En esta entrada se ha elaborado todo el proceso para obtener los estimados derivados de la aplicación del método de Mínimos Cuadrados Ordinarios (MCO) para un modelo de regresión simple.
Debe notarse que en este punto solo se ha explicado la mecánica matemática de los MCOs y algo de inferencia estadística sin embargo, nada se ha dicho respecto a si los estimados encontrados son o no causales. Nótese que el análisis causal no es mecánico y no existe una fórmula matemática para saber si esto se cumple o no.
De forma práctica, es trabajo del econometrista hacer sus mejores esfuerzos para diseñar el experimento o encontrar la manera de estimar, bajo ciertas condiciones, parámetros causales.
Dicha causalidad, principalmente, viene como respuesta a la siguiente pregunta: ¿Se cumple en mi modelo el supuesto de exogeneidad? Es decir, ¿se cumple que $E(u|x)=0$? Esto, de forma forma práctica, no es más que preguntarse si existe alguna variable que causa/influye tanto en la variable $Y$ como en la $X$ de interés y la cual ha sido omitida del análisis con lo cual esa variable ahora está en el error $u$ invalidando el supuesto de exogeneidad.