Sumatoria
Definición
La sumatoria, $\displaystyle\sum_{i=1}^{n}$, es un operador matemático que nos permite sumar una secuencia de números.
Este operador contiene un iterador o índice que usualmente se denota como $i$ o $j$, aunque puede ser cualquier letra. Este indica desde dónde se debe comenzar a contar. También se coloca una $n$ para indicar el último número de la secuencia.
Si se tuviera una tabla, este operador podría indicar que se deben sumar todas las filas o todas las columnas. Por ejemplo:
| # | Día | Ingreso (Bs.) |
|---|---|---|
| 1 | Lunes | 50 |
| 2 | Martes | 70 |
| 3 | Miércoles | 40 |
| 4 | Jueves | 20 |
| 5 | Viernes | 100 |
Donde nos interesa calcular el total del ingreso ganado durante la semana.
$$\begin{aligned} \sum_{i=1}^{5}Ing_i &= Ing_1 + Ing_2 + Ing_3 + Ing_4 + Ing_5 \\ &= 50 + 70 + 40 + 20 + 100 \\ &= 280 \end{aligned}$$
En $\mathrm{R}$ esto se se calcula como:
ingreso <- c(50, 70, 40, 20, 100)
base::sum(ingreso)
## [1] 280
Claramente hay algunos más complejos, pero simplemente se debe seguir lo que indica el operador:
$$\begin{aligned} \sum_{k=3}^{5}(2k-3)^{2} &= (2\cdot3-3)^{2}+(2\cdot4-3)^{2}+(2\cdot5-3)^{2} \\ &= 9 + 25 + 49 \\ &= 83 \end{aligned}$$
Ejercicio
Desarrolle la siguiente sumatoria:
$$\sum_{i=1}^{4}(y_i-\beta_0-\beta_1x_i)^{2} $$
Donde $\beta_0 = 1$, $\beta_1 = 1.5$ y, además:
| Id | x | y |
|---|---|---|
| 1 | 3 | 8 |
| 2 | 2 | 5 |
| 3 | 5 | 10 |
| 4 | 3 | 9 |
Reglas
Algunas reglas de la sumatoria son:
-
Aditividad: $$\sum_{i=1}^{n}(a_i + b_i) = \sum_{i=1}^{n}a_i +\sum_{i=1}^{n}b_i $$
-
Homogeneidad: $$\sum_{i=1}^{n}c \cdot a_i = c \sum_{i=1}^{n}a_i $$
En el caso de que $a_i = 1$ para todo $i$, se tiene $$ \sum_{i=1}^{n} c = n\cdot c$$
Doble sumatoria
La doble sumatoria, denotada como $\displaystyle\sum_{i=1}^{n} \sum_{j=1}^{k}$ permite tener en cuenta dos índices o iteradores. Por ejemplo, si se tuviera una tabla, este operador indicaría que se sumen todas las filas y las columnas.
Por ejemplo, imagine que se desea sumar las ventas totales que un conjunto de vendedores ha realizado durante la semana:
| Vendedor | Lunes | Martes | Miércoles | Jueves | Viernes |
|---|---|---|---|---|---|
| Juan | 100 | 120 | 140 | 80 | 20 |
| María | 50 | 800 | 0 | 150 | 200 |
| Perico | 0 | 30 | 120 | 0 | 400 |
| Martina | 500 | 0 | 0 | 250 | 0 |
Nótese que se tienen $4$ vendedores y $5$ días. Notacionalmente se tiene: $$\sum_{i=1}^{4}\sum_{j=1}^{5}ventas_{ij} = ventas_{Ju, Lun}+ ventas_{Ju, Mar}+…+ ventas_{Mart, Vie}$$
Funciones
Funciones univariadas
Conceptualmente las funciones, denotadas como $y = f(x)$, indican una relación de dependencia entre dos variables.
Definición. Una función de una variable real $x$ con un dominio $\mathcal{D}$ es una regla $x \rightarrow f(x)$ que asigna a único número real $f(x)$ a cada número real $x$ en $\mathcal{D}$. Cuando $x$ cambia dentro del todo su dominio, el conjunto de todos los posibles valores resultantes de $f(x)$ es llamado el rango de $f$ .
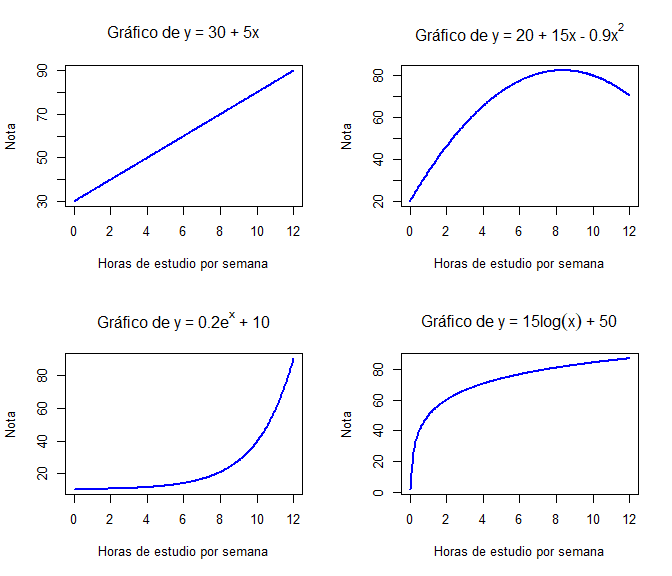
Por ejemplo, supongamos que $y = \textit{nota econometría}$ y $x = \textit{horas estudiadas por semana}$. ¿Cómo graficaría esta relación?
Intuición gráfica
par(mfrow = c(2,2))
curve( 30+5*x, from=0, to=12, n=300,
xlab="Horas de estudio por semana", ylab="Nota", col="blue", lwd=2,
main= expression(paste("Gráfico de y = 30 + 5x")))
curve( 20 + 15*x - 0.9*x^2 , from=0, to=12, n=300,
xlab="Horas de estudio por semana", ylab="Nota", col="blue", lwd=2,
main= expression(paste("Gráfico de y = 20 + 15x - 0.9", x^2)))
curve( 0.2*exp(0.5*x)+ 10, from=0, to=12, n=300,
xlab="Horas de estudio por semana", ylab="Nota", col="blue", lwd=2,
main= expression(paste("Gráfico de y = 0.2", e^x, " + 10")))
curve(15*log(x)+50, from = 0, to= 12, n = 300,
xlab="Horas de estudio por semana", ylab="Nota", col="blue", lwd=2,
main= expression(paste("Gráfico de y = 15", log(x), " + 50")))
Funciones multivariadas
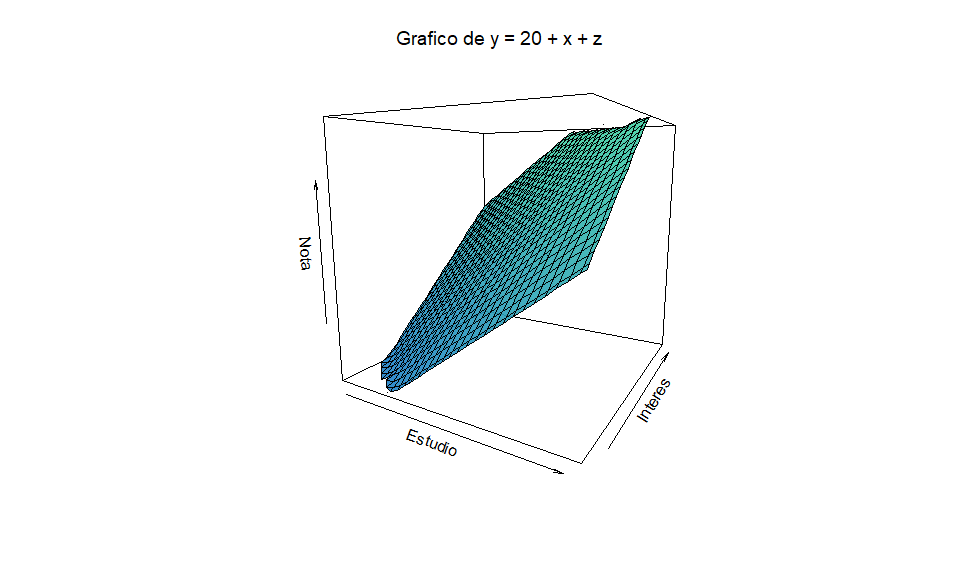
Anteriormente vimos que una función interesante es la que relaciona $y = \textit{nota econometría}$ con $x = \textit{horas estudiadas por semana}$.
Dependiendo de la forma de $f(\cdot)$, el comportamiento de $y$, podría variar. Sin embargo, esta relación no tomaba en cuenta otras variables que podrían estar modificando la relación entre $x$ y $y$. Una de esas variables podría ser $z = \textit{interés por la materia}$.
¿Cómo influye esta tercera variable $z$ en la relación entre las notas, $y$, y las horas de estudio, $x$? Por ejemplo, para las mismas horas de estudio, un estudiante que tiene más interés por la materia que otro, tendrá mejor o peor nota? ¿Por qué?
Lo anterior se puede capturar con una función del tipo $y = f(x,z)$.
Intuición gráfica
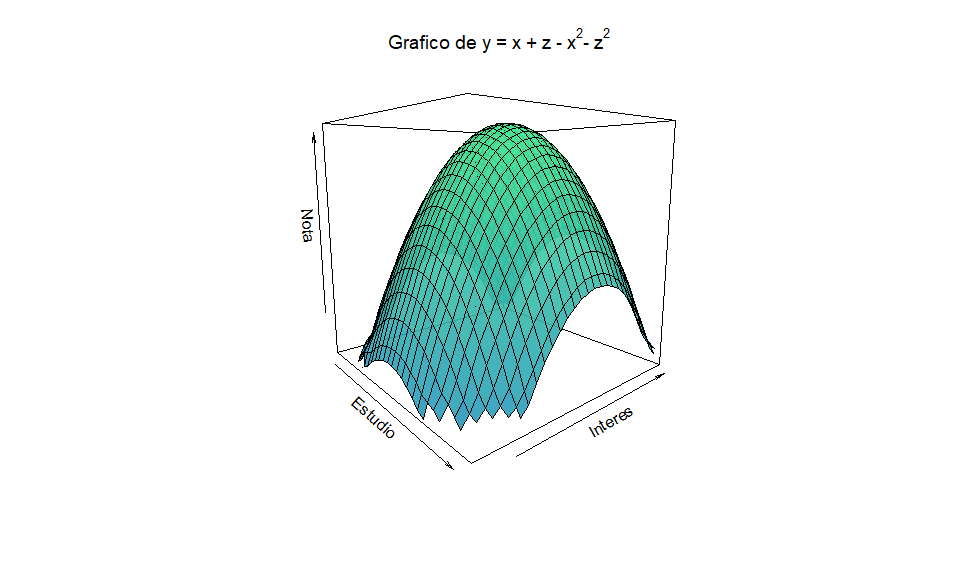
Intuición: Rendimientos decrecientes
Derivadas
Una función $y = f(x)$ es diferenciable si es continua en un punto, digamos $x = x_{0}$ y, a medida que se incrementa $x$ el límite de la función existe en dicho punto:
$$f’(x_0)= \lim_{\Delta x \rightarrow 0} \frac{\Delta y}{\Delta x} \equiv \lim_{\Delta x \rightarrow 0} \frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}$$
Otra forma de entender la derivada es como la pendiente de la función cuando la variable $x$ se incrementa en una unidad muy pequeña.
Derivadas de funciones univariadas
Derivada de una constante
La derivada de una función constante $y = k$ o $f(x)=k$ es $0$. Esto se puede expresar de muchas formas: $$\frac{dy}{dx} = \frac{dk}{dx} =0 \qquad \text{;} \qquad f’(x)=0 $$
Alternativamente puede expresarse como:
$$\frac{d}{dx}y =\frac{d}{dx}f(x)= \frac{d}{dx}k = 0 $$
Derivada de una potencia
La derivada de la función $y = f(x) = x^n$ es $nx^{n-1}$, simbólicamente: $$\frac{d}{dx}x^n = nx^{n-1} $$
Derivada de una potencia: generalización
Es posible combinar ambas reglas. Por ejemplo, cuando una constante $c$ aparece dentro de una función que tiene una potencia, $y=f(x)=cx^{n}$: $$\frac{d}{dx}cx^n = cnx^{n-1} $$
Derivada de un logaritmo
La derivada de una función logarítmica del tipo $y = \ln(x)$ es: $$\frac{d}{dx}\ln{y} = \frac{1}{x}$$
Generalizando: $$\frac{d}{dx} \ln f(x) = \frac{f’(x)}{f(x)}$$
Por ejemplo, la derivada de $y = \ln(6x^2)$ es: $$\frac{d}{dx}\ln(6x^2)= \frac{12x}{6x^2} = \frac{2}{x}$$
Derivada de un producto
La derivada del producto de dos funciones diferenciables es igual a la primer función multiplicada por la derivada de la segunda más la segunda función multiplicada por la derivada de la primera: $$ \frac{d}{dx}\big[f(x) g(x)\big] = f(x) \frac{d}{dx} g(x) +g(x) \frac{d}{dx} f(x)$$
A veces es más sencilla expresarla como $$ \frac{d}{dx}\big[f(x) g(x)\big] = f’(x) g(x) +f(x) g’(x) $$
Derivadas de funciones multivariadas
Regla de la cadena
Imagine que se tiene una función $z = f(y)$ y, a su vez, $y$ otra función que depende de $x$, es decir, $y = g(x)$. Así, $z = f\big(g(x)\big)$ ¿Cómo obtenemos la derivada de $z$ respecto a $x$? $$\frac{dz}{dx} = \frac{dz}{dy}\frac{dy}{dx} = f’(y)g’(x) $$
Esta regla se conoce como de la cadena porque la respuesta final del cambio en $x$ sobre $z$ se obtiene por pasos: $$\Delta x \xrightarrow{via ; g} \Delta y \xrightarrow{via ; f} \Delta z$$
Por ejemplo, si $z = 3y^2$ y, además, $y = 2x+5$, encuentre $\frac{dz}{dx}$ $$\frac{dz}{dx} = \frac{dz}{dy} \frac{dy}{dx} = 6y(2) = 12(2x+5) $$
Derivadas parciales
Cuando se tiene una función con más de una variable independiente, el concepto de derivada debe modificarse. ¿Por qué?
Si la derivada se interpreta como el cambio en $y$ cuando $x$ se incrementa una pequeña unidad, ¿qué sucede, por ejemplo, con $z$?
Más generalmente, considere una función que depende de $n$ variables: $$ y = f(x_1, x_2, …, x_n)$$
Donde todas las $x_i$ ($i = 1,2,…,n$) son independientes las unas de las otras.
Si la variable $x_1$ se incrementa $\Delta x_1$, entonces las restantes $x_2, x_3,…,x_n$ se mantienen constantes o fijas.
Así, se puede expresar matemáticamente como: $$\frac{\Delta y}{\Delta x_1} = \frac{f(x_1+\Delta x_1, x_2, …, x_n)-f(x_1,x_2,…,x_n)}{\Delta x_1} $$
Si tomamos el límite de esta expresión cuando $\Delta x_1 \rightarrow 0$, este límite se conoce como derivada parcial.
Matemáticamente, se utiliza la letra griega delta minúscula, para denotarlo: $$\frac{\partial}{\partial x_i}y \equiv f_i \equiv \lim_{\Delta x_i \rightarrow 0} \frac{\Delta y}{\Delta x_i}$$
Ejemplo
Dada la función $y = f(x_1, x_2) = 3x^{2}_{1} + x_{1}x_{2} + 4 x_{2}^{2}$ , encuentre sus derivadas parciales.
$$\begin{aligned} \frac{\partial y}{\partial x_1} \equiv f_1 &= 6x_1 + x_2 \\ \frac{\partial y}{\partial x_2} \equiv f_2 &= x_1 + 8x_2 \end{aligned}$$
Intuición gráfica
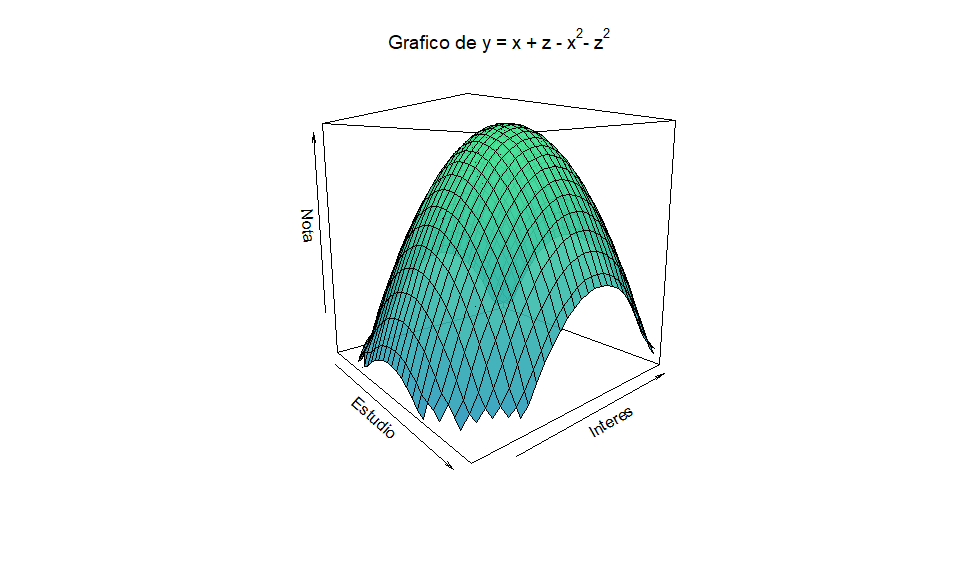
Optimización
Intuición
La optimización hace referencia a la eficiencia. Nótse que cuando elegimos, los seres humanos tratamos siempre de tomar la mejor decisión, dada las restricciones que enfrentamos en ese momento. Es decir, tratamos de tomar la elección óptima.
Algunas veces esta decisión implica sacar el máximo provecho de esa situación y, otras veces, implica realizar el mínimo esfuerzo para alcanzar el resultado deseado.
Máximos (mínimos) relativos
Regularmente, en todo problema de optimización se tiene una función objetivo y al menos una variable de elección.
El problema se reduce a encontrar los valores de dichas variables que maximicen (o minimicen) dicha función.
Por ejemplo, ¿dónde se encuentra el óptimo en la siguiente función?
curve(x^3 - 6*x^2+9*x+10, from=0, to=3,n=200,
xlab="Horas de estudio por semana", ylab="Nota", col="blue", lwd=2,
main= expression(paste("Grafico de y = 10 + 9x - 6", x^2,"+ ", x^3)))
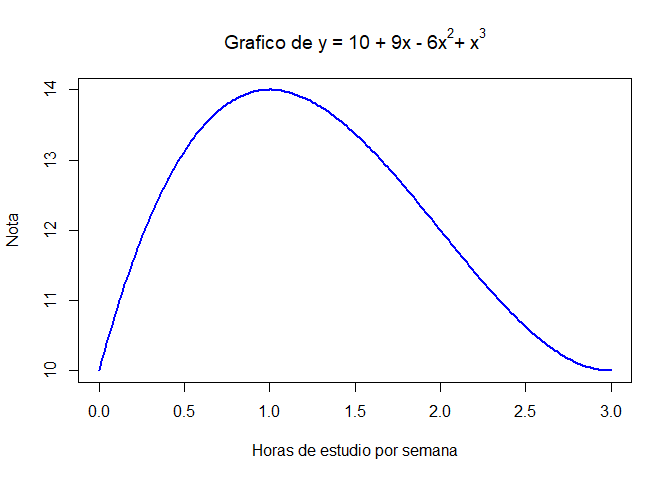
¿Y en la siguiente?
curve(x^3 - 6*x^2+9*x+10, from=0, to=4,n=200,
xlab="Horas de estudio por semana", ylab="Nota", col="blue", lwd=2,
main= expression(paste("Grafico de y = 10 + 9x - 6", x^2,"+ ", x^3)))
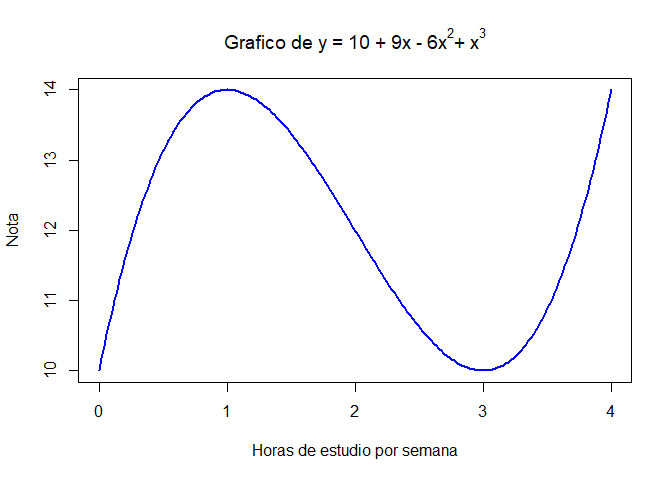
Criterios
Habiendo visto lo anterior, se necesitan criterios matemáticos para encontrar un máximo o un mínimo.
La condición necesaria o Condición de Primer Órden (CPO) para la existencia de un máximo o mínimo es que la primera derivada se $0$. Es decir: $$f’(x) = 0$$
Dado que esto identifica tanto un máximo como un mínimo, la condición suficiente o Condición de Segundo Orden (CSO) para un máximo es: $$f’’(x) < 0$$
Para un mínimo es: $$f’’(x)>0$$
Resuelva
Encuentre el máximo/mínimo de la siguiente función: $$y = 5 + 3x + x^2$$ Encuentre el máximo/mínimo de la siguiente función: $$y = 10 +9x - 6x^2 + x^3$$
Encuentre el máximo/mínimo de: $$z = 5 + 8x + 7y + 4xy -2x^2- 5y^2$$
Ejemplo
El ejercicio se plantea como: $$\max_{x,y} z =5 + 8x + 7y + 4xy -2x^2- 5y^2$$
Para resolverlo, debemos tomar las primeras derivadas parciales o CPO. $$\begin{aligned} \begin{cases} \frac{\partial z}{\partial x} &= 8 + 4y -4x = 0 \\ \frac{\partial z}{\partial y} &= 7 + 4x - 10y = 0 \end{cases} \end{aligned}$$
Estas condiciones generan un sistema de ecuaciones lineales que debe resolverse para encontrar los puntos críticos, es decir, los puntos donde puede existir un máximo o un mínimo.
Para esto, se despeja $x$ en la primera ecuación, $x=\color{green}{2 + y}$, y se reemplaza en la segunda: $$\begin{aligned} 7 + 4x - 10y \\ 7+ 4 \color{green}{(2+y)} - 10y &= 0 \\ 7 + 8 +4y-10y &= 0 \\ y &= \color{blue}{\frac{5}{2}} \end{aligned}$$
Reemplazando este resultado en $\frac{\partial z}{\partial x}$: $$\begin{aligned} 8 + 4y -4x &= 0 \\ 8+ 4\color{blue}{\frac{5}{2}} - 4x &= 0 \\ x &= \color{orange}{\frac{9}{2}} \end{aligned}$$
Por tanto, el par ordenado $\Big(\color{orange}{\frac{9}{2}},\color{blue}{\frac{5}{2}}\Big)$ representa los valores críticos. Ahora, ¿cómo sabemos si es un máximo o mínimo?
En el caso de una función con más de dos variables independientes las condiciones son:
| Condición | Máximo | Mínimo |
|---|---|---|
| CPO | $f_x = f_y = 0$ | $f_x = f_y = 0$ |
| CSO | $f_{xx}, f_{yy} < 0$ | $f_{xx}, f_{yy} > 0$ |
| $f_{xx} \cdot f_{yy} > f_{xy}^{2}$ | $f_{xx} \cdot f_{yy} > f_{xy}^{2}$ |
Tomando las segundas derivadas y las derivadas cruzadas se tiene: $$\begin{aligned} \begin{cases} \frac{\partial^{2} z}{\partial x^{2}} &= -4 \\ \frac{\partial^{2} z}{\partial y^{2}} &= -10 \\ \frac{\partial^{2} z}{\partial x \partial y} &= 4 \\ \frac{\partial^{2} z}{\partial y \partial x} &= 4 \\ \end{cases} \end{aligned}$$
Donde se verifica que $f_{xx}, f_{yy} < 0$ y, además $f_{xx} \cdot f_{yy} > f_{xy}^{2}$. Por tanto, se ha encontrado un máximo.
Bibliografía
- Chiang A. C. & Wainwright K. (2005). Fundamental methods of mathematical economics (4th ed.). McGraw-Hill/Irwin.
- Sydsaeter K., Hammond P., Strom A. & Carvajal A. (2021). Essential Mathematics for Economic Analysis (6th ed.). Pearson Education.