Introducción: dependencias
En la presente entrada se reproducirá el problema planteado en clases respecto a las muertes por tráfico y su relación con el consumo de bebidas alcohólicas. El detalle se puede encontrar en Stock & Watson (2020).
Los paquetes que se utilizarán:
install.packages("tidyverse")
install.packages("AER")
install.packages("plm")
install.packages("lmtest")
install.packages("sandwich")
install.packages("modelsummary")
Una vez instalados los paquetes, procedemos a llamarlos:
library(tidyverse)
library(AER)
library(plm)
library(lmtest)
library(sandwich)
library(modelsummary)
Cargar los datos
Para cargar los datos, se utiliza la función data:
data("Fatalities",package = "AER")
Para entender los datos:
str(Fatalities)
'data.frame': 336 obs. of 34 variables:
$ state : Factor w/ 48 levels "al","az","ar",..: 1 1 1 1 1 1 1 2 2 2 ...
$ year : Factor w/ 7 levels "1982","1983",..: 1 2 3 4 5 6 7 1 2 3 ...
$ spirits : num 1.37 1.36 1.32 1.28 1.23 ...
$ unemp : num 14.4 13.7 11.1 8.9 9.8 ...
$ income : num 10544 10733 11109 11333 11662 ...
$ emppop : num 50.7 52.1 54.2 55.3 56.5 ...
$ beertax : num 1.54 1.79 1.71 1.65 1.61 ...
$ baptist : num 30.4 30.3 30.3 30.3 30.3 ...
$ mormon : num 0.328 0.343 0.359 0.376 0.393 ...
$ drinkage : num 19 19 19 19.7 21 ...
$ dry : num 25 23 24 23.6 23.5 ...
$ youngdrivers: num 0.212 0.211 0.211 0.211 0.213 ...
$ miles : num 7234 7836 8263 8727 8953 ...
$ breath : Factor w/ 2 levels "no","yes": 1 1 1 1 1 1 1 1 1 1 ...
$ jail : Factor w/ 2 levels "no","yes": 1 1 1 1 1 1 1 2 2 2 ...
$ service : Factor w/ 2 levels "no","yes": 1 1 1 1 1 1 1 2 2 2 ...
$ fatal : int 839 930 932 882 1081 1110 1023 724 675 869 ...
$ nfatal : int 146 154 165 146 172 181 139 131 112 149 ...
$ sfatal : int 99 98 94 98 119 114 89 76 60 81 ...
$ fatal1517 : int 53 71 49 66 82 94 66 40 40 51 ...
$ nfatal1517 : int 9 8 7 9 10 11 8 7 7 8 ...
$ fatal1820 : int 99 108 103 100 120 127 105 81 83 118 ...
$ nfatal1820 : int 34 26 25 23 23 31 24 16 19 34 ...
$ fatal2124 : int 120 124 118 114 119 138 123 96 80 123 ...
$ nfatal2124 : int 32 35 34 45 29 30 25 36 17 33 ...
$ afatal : num 309 342 305 277 361 ...
$ pop : num 3942002 3960008 3988992 4021008 4049994 ...
$ pop1517 : num 209000 202000 197000 195000 204000 ...
$ pop1820 : num 221553 219125 216724 214349 212000 ...
$ pop2124 : num 290000 290000 288000 284000 263000 ...
$ milestot : num 28516 31032 32961 35091 36259 ...
$ unempus : num 9.7 9.6 7.5 7.2 7 ...
$ emppopus : num 57.8 57.9 59.5 60.1 60.7 ...
$ gsp : num -0.0221 0.0466 0.0628 0.0275 0.0321 ...
Antes y después
Estimación de corte transversal con lm()
Como se observa, existe la variable $fatal$ que son los accidentes de tránsito y existe la variable $pop$ que es la población de cada Estado. Para obtener la tasa de fatalidad, la cual se constituirá en nuestra variable objetivo o $Y$, necesitamos definir:
Fatalities$fatal_rate <- Fatalities$fatal / Fatalities$pop * 10000
En primer lugar, vamos a explorar la relación entre estas variables en dos distintos períodos: $1982$ vs. $1988$. Para esto, vamos a hacer un subset de los datos:
Fatalities1982 <- subset(Fatalities, year == "1982")
Fatalities1988 <- subset(Fatalities, year == "1988")
Ahora, vamos a correr un modelo de regresión, lm que relaciona la tasa de fatalidad, $fatal\_rate$, con los impuestos al alcohol, en particular los impuestos en USD a la caja de cerveza, $beertax$:
fatal1982_mod <- lm(fatal_rate ~ beertax, data = Fatalities1982)
fatal1988_mod <- lm(fatal_rate ~ beertax, data = Fatalities1988)
Visualizando el resultado con modelsummary:
modelsummary::modelsummary(list("OLS 1982" =fatal1982_mod,
"OLS 1988" = fatal1988_mod),
gof_map = c("nobs","r.squared"),
coef_map = c("beertax", "stateal","stateaz"),
estimate = "{estimate}{stars}",
output = "markdown")
| OLS 1982 | OLS 1988 | |
|---|---|---|
| beertax | 0.148 | 0.439* |
| (0.188) | (0.164) | |
| Num.Obs. | 48 | 48 |
| R2 | 0.013 | 0.134 |
Adicionalmente, para evitar problemas en el cálculo de los errores estándar, vamos a utilizar una clase de errores robustos a la heterocedasticidad:
modelsummary::modelsummary(list("OLS 1982" =fatal1982_mod,
"OLS 1988" = fatal1988_mod),
gof_map = c("nobs","r.squared"),
coef_map = c("beertax", "stateal","stateaz"),
estimate = "{estimate}{stars}",
vcov = sandwich::vcovHC,
output= "markdown")
| OLS 1982 | OLS 1988 | |
|---|---|---|
| beertax | 0.148 | 0.439** |
| (0.145) | (0.142) | |
| Num.Obs. | 48 | 48 |
| R2 | 0.013 | 0.134 |
Gráficamente:
ggplot(Fatalities1982,aes(x=beertax,y=fatal_rate))+
geom_point(color="steelblue",size=2)+
geom_smooth(method='lm', formula= y~x, se=F,color="black",size=0.9)+
labs(title="Tasa de muertes por tráfico e Impuestos a la cerveza en 1982",
x = "\nImpuesto sobre la cerveza (USD de 1988)",
y = "Tasa de mortalidad (muertes por cada 10,000 habs.)\n")+
scale_y_continuous(limits = c(0,5))+
scale_x_continuous(limits = c(0,3)) +
theme_bw()
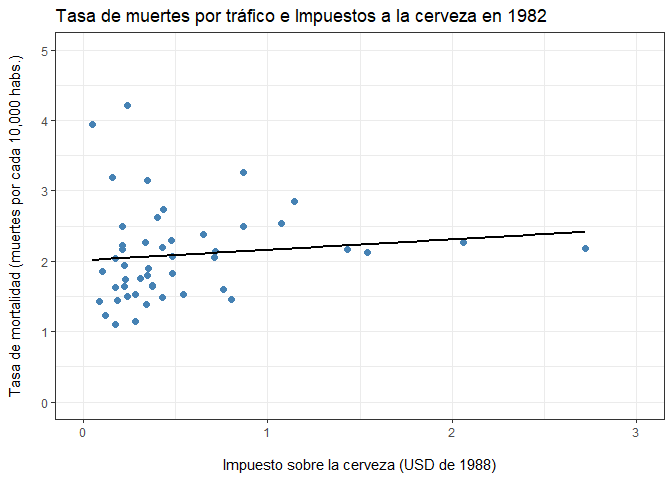
En el caso de 1988:
ggplot(Fatalities1988,aes(x=beertax,y=fatal_rate))+
geom_point(color="steelblue",size=2)+
geom_smooth(method='lm', formula= y~x, se=F,color="black",size=0.9)+
labs(title="Tasa de muertes por tráfico e Impuestos a la cerveza en 1988",
x = "\nImpuesto sobre la cerveza (USD de 1988)",
y = "Tasa de mortalidad (muertes por cada 10,000 habs.)\n")+
scale_y_continuous(limits = c(0,5))+
scale_x_continuous(limits = c(0,3)) +
theme_bw()
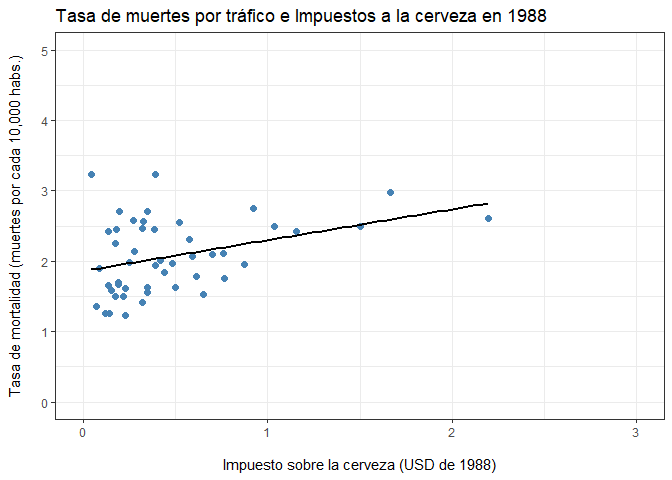
¿Cómo se interpretan estos hallazgos?
El modelo de “Antes” vs “Después”
En clase habíamos visto que cuando los datos de cada estado se obtienen para $T=2$ períodos de tiempo, es posible comparar valores de la variable dependiente en el segundo período con los valores del primer período.
Al centrarse en los cambios en la variable dependiente, este “antes y después” o la comparación de “diferencias”, en efecto, mantiene constantes los factores no observados que difieren de un estado al siguiente, pero no cambian con el tiempo dentro del estado:
Básicamente, si suponemos que hay $Z_i$ factores que son diferentes entre las distintas entidades $i$ pero son constantes en el tiempo, podremos especificar un modelo, para cada año, como:
$$\begin{array}{c} \begin{aligned} FatalityRate_{i1982} &= \beta_{0} + \beta_{1}BeerTax_{i1982} + \beta_{2}Z_{i} + u_{i1982} \\ FatalityRate_{i1988} &= \beta_{0} + \beta_{1}BeerTax_{i1988} + \beta_{2}Z_{i} + u_{i1988} \end{aligned} \end{array}$$
Concentrándonos sólo en las diferencias tenemos: $$FatalityRate_{i1988} - FatalityRate_{i1982}= \beta_{1} (BeerTax_{i1988} - BeerTax_{i1982}) + u_{i1988} - u_{i1982}$$
Entonces, este modelo “en diferencias” puede ser estimado utilizando MCO:
En primer lugar, creamos las variables en diferencias en cada uno de los dataframes:
diff_fatal_rate <- Fatalities1988$fatal_rate - Fatalities1982$fatal_rate
diff_beertax <- Fatalities1988$beertax - Fatalities1982$beertax
Con estas variables, armamos el modelo de regresión:
fatal_diff_mod <- lm(diff_fatal_rate ~ diff_beertax)
modelsummary::modelsummary(list("Modelo en diffs." = fatal_diff_mod),
gof_map = c("nobs","r.squared"),
coef_map = c("diff_beertax","(Intercept)"),
estimate = "{estimate}{stars}",
vcov = sandwich::vcovHAC,
output = "markdown")
| Modelo en diffs. | |
|---|---|
| diff_beertax | -1.041** |
| (0.333) | |
| (Intercept) | -0.072 |
| (0.056) | |
| Num.Obs. | 48 |
| R2 | 0.119 |
Nota: Incluir el intercepto en este modelo permite que la media en la tasa de fatalidad varíe entre 1982 y 1988.
De forma gráfica:
diff_fatalities = data.frame(diff_fatal_rate,diff_beertax)
ggplot(diff_fatalities,aes(x=diff_beertax,y=diff_fatal_rate))+
geom_point(color="steelblue",size=2)+
geom_smooth(method='lm', formula= y~x, se=F,color="black",size=0.9)+
labs(title="Cambio en tasa de muertes por tráfico e Impuestos a la cerveza en 1982-1988",
x = "\nCambio en Impuesto sobre cerveza (USD de 1988)",
y = "Cambio en Tasa de Mortalidad (muertes por 10,000 habs.)\n")+
scale_y_continuous(limits = c(-1.5,1))+
scale_x_continuous(limits = c(-0.6,0.6)) +
theme_bw()
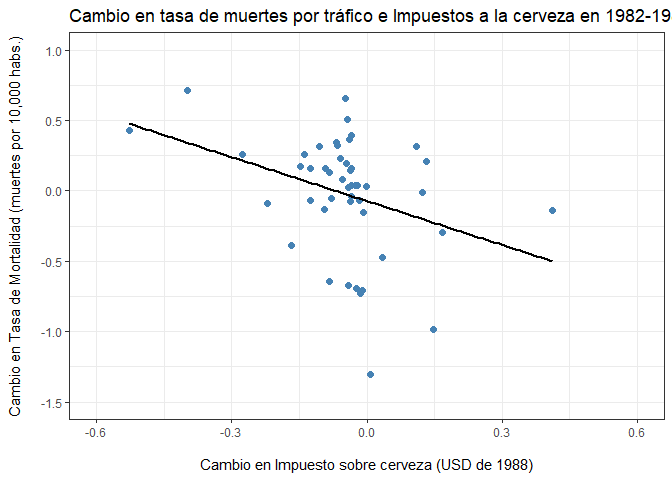
¿Cómo se interpreta esta ecuación? Para tener un poco de contexto (o alguna forma de comparar) calculemos:
mean(Fatalities$fatal_rate)
[1] 2.040444
Y la pregunta de rigor… ¿es el coeficiente estimado, causal?
El modelo de Panel con Efectos Fijos
El modelo
Considere el modelo “antes y después” con la variable dependiente ($FatalityRate$) y el regresor observado ($BeerTax$) denotados como $Y_{it}$ y $X_{it}$, respectivamente: $$FatalityRate_{it}=\beta_{0} + \beta_{1}BeerTax_{it} + \beta_{2}Z_{i} + u_{it}$$
Donde $Z_{i}$ es una variable no observada que varía de un Estado a otro pero no cambia con el tiempo (time-invariant heterogeneity).
Debido a que $Z_{i}$ varía de un estado a otro pero es constante en el tiempo, el modelo de regresión poblacional se puede interpretar como si tuviera $n$ interceptos.
Sea $\alpha_{i}= \beta_{0} + \beta_{2}Z_{i}$. Entonces la ecuación se convierte en: $$FatalityRate_{it}=\beta_{1}BeerTax_{it} + \alpha_{i} + u_{it}$$
El modelo de regresión de efectos fijos, en el que se tratan $\alpha_{1},…, \alpha_{n}$ como interceptos desconocidos a estimar, uno para cada Estado.
De forma equivalente, este modelo puede ser reescrito como: $$Y_{it}=\beta_{0} + \beta_{1}X_{it} + \gamma_{2}D2_{i} + \gamma_{3}D3_{i} + … + \gamma_{n}Dn_{i} + u_{it}$$
Donde $\beta_{0},\beta_{1}, \gamma_{2},…, \gamma_{n}$ son coeficientes desconocidos para estimar.
Una forma de entender esto es imaginarse el conjunto de datos:
| Año | Estado | $D_1$ | $D_2$ | $D_3$ |
|---|---|---|---|---|
| 1982 | Alabama | $1$ | $0$ | $0$ |
| 1983 | Alabama | $1$ | $0$ | $0$ |
| 1984 | Alabama | $1$ | $0$ | $0$ |
| 1982 | Arizona | $0$ | $1$ | $0$ |
| 1983 | Arizona | $0$ | $1$ | $0$ |
| 1984 | Arizona | $0$ | $1$ | $0$ |
| 1982 | California | $0$ | $0$ | $1$ |
| 1983 | California | $0$ | $0$ | $1$ |
| 1984 | California | $0$ | $0$ | $1$ |
Donde las $D_i$ son los “efectos fijos”.
Tomando los promedios en ambos lados de: $$Y_{it}=\beta_{1}X_{it} + \alpha_{i} + u_{it}$$
Se obtiene:
$$\begin{aligned} \frac{1}{n} \sum_{i=1}^n Y_{it} =& \beta_1 \frac{1}{n} \sum_{i=1}^n X_{it} + \frac{1}{n} \sum_{i=1}^n a_i + \frac{1}{n} \sum_{i=1}^n u_{it} \\ \overline{Y} =& \beta_1 \overline{X}_i + \alpha_i + \overline{u}_i \end{aligned}$$
Si se sustrae este resultado de la ecuación inicial, se tiene:
$$ \begin{aligned} Y_{it} - \overline{Y_{i}} =& \beta_{1}(X_{it} - \overline{X_{i}}) + (u_{it} - \overline{u_{i}}) \\ \overset{\sim}{Y_{it}} =& \beta_{1} \overset{\sim}{X_{it}} + \overset{\sim}{u_{it}} \end{aligned}$$
El estimador de $\beta_1$ obtenido es equivalente al obtenido estimando las $n-1$ dummies y el intercepto.
Aplicación “manual”
Una forma de aplicar el modelo es simplemente aplicar la función lm y estimar un regresor para cada estado:
$$FatalityRate_{it} = \beta_1 BeerTax_{it} + StateFixedEffects + u_{it}$$
Donde nos interesa estimar $\beta_1$.
Nota: Para que esto funcione, las potenciales variables dummy, como state tienen que estar definidas como factor.
fatal_fe_lm_mod <- lm(fatal_rate ~ beertax + state - 1, data = Fatalities)
modelsummary::modelsummary(list("OLS con efectos fijos"=fatal_fe_lm_mod),
gof_map = c("nobs","r.squared"),
coef_map = c("beertax", "stateal","stateaz"),
estimate = "{estimate}{stars}",
vcov = sandwich::vcovHC,
output = "markdown")
| OLS con efectos fijos | |
|---|---|
| beertax | -0.656** |
| (0.229) | |
| stateal | 3.478*** |
| (0.394) | |
| stateaz | 2.910*** |
| (0.152) | |
| Num.Obs. | 336 |
| R2 | 0.993 |
Nótese que, al incluir los efectos fijos, el estimado sube de $-1.041$ a $-0.656$, al igual que pierde significancia. Esto nos da una idea de que, el estimador, al no incluir los efectos fijos, contenía un sesgo hacia arriba.
Alternativamente, podemos ocupara el estimador entity-demeaned: $$\overset{\sim}{FatalityRate} = \beta_1 \overset{\sim}{BeerTax_{it}} + u_{it}$$
Para esto, tenemos que formar un nuevo dataframe que tome en cuenta las variables desprovistas de su media. Para esto vamos a ocupar la función with() y ave() (esta última es bastante conveniente para tomar promedios sobre grupos):
Fatalities_demeaned <- with(Fatalities,
data.frame(
fatal_rate = fatal_rate - ave(fatal_rate, state),
beertax = beertax - ave(beertax, state)))
Ahora, observamos el dataset sin medias:
head(Fatalities_demeaned)
fatal_rate beertax
1 -0.28426713 -0.08441320
2 -0.06414705 0.16519805
3 -0.07619715 0.09049293
4 -0.21914718 0.02874967
5 0.25651277 -0.01388565
6 0.30596278 -0.06379274
Ahora, estimamos la regresión usual utilizando lm():
modelsummary::modelsummary(list("OLS con efectos fijos"=lm(fatal_rate ~ beertax - 1, data = Fatalities_demeaned)),
gof_map = c("nobs","r.squared"),
coef_map = c("beertax", "stateal","stateaz"),
estimate = "{estimate}{stars}",
vcov = sandwich::vcovHC,
output = "markdown")
| OLS con efectos fijos | |
|---|---|
| beertax | -0.656*** |
| (0.195) | |
| Num.Obs. | 336 |
| R2 | 0.041 |
Donde básicamente obtenemos los mismos coeficientes. Sin embargo, al estimar menos coeficientes en el segundo modelo, conseguimos errores estándar más preciso.
Aplicación “automática”
Alternativamente, existen rutinas automáticas implementadas en R como plm::plm() que ya incorporan los algoritmos respectivos.
Como ocurre en el caso de lm(), se tiene que especificar la fórmula de regresión y los datos que van a ser consumidos.
Adicionalmente, se necesita pasar un vector con los nombres de la entidad y un identificador del tiempo o período de los datos al argumento index.
Por ejemplo, para $Fatalities$, la variable identificador para las entidades es $state$ y la variable identificador temporal es $year$.
Además, como el estimador de efectos fijos es a veces llamado within estimador, colocamos model = "within".
# estimación del estimador de efectos fijos con plm()
fatal_fe_mod <- plm::plm(fatal_rate ~ beertax,
data = Fatalities,
index = c("state", "year"),
model = "within")
# colocar el resumen de la regresión con errores estándar robustos
modelsummary::modelsummary(list("Panel con efectos fijos"=fatal_fe_mod),
gof_map = c("nobs","r.squared"),
coef_map = c("beertax", "stateal","stateaz"),
estimate = "{estimate}{stars}",
vcov = sandwich::vcovHC,
output = "markdown")
| Panel con efectos fijos | |
|---|---|
| beertax | -0.656* |
| (0.288) | |
| Num.Obs. | 336 |
| R2 | 0.041 |
En esta implementación, el coeficiente es $-0.6559$. Se debe notar que plm() usa el algoritmo entity-demeaned y, por lo tanto, no reporta los coeficientes de las variables dummy.
La ecuación estimada es: $$\begin{aligned} \widehat{FatalityRate} = -\underset{(0.29)}{0.66} \times BeerTax + StateFixedEffects \end{aligned}$$
El modelo de Panel con Efectos Fijos Temporales
Así como con los efectos fijos para cada entidad se pueden controlar las variables que son constantes durante tiempo pero difieren entre entidades, así también los efectos fijos temporales (time fixed effects) pueden controlar las variables que son constantes entre entidades pero cambian con el tiempo.
Una forma de entender el modelo, cuando solo hay efectos fijos temporales es: $$Y_{it} = \beta_0 + \beta_1 X_{it} + \delta_2 B2_t + \cdots + \delta_T BT_t + u_{it}$$
Donde se colocan $T-1$ variables dummy, una por cada periodo.
Alternativamente, lo anterior se puede resumir como: $$Y_{it} = \beta_{1}X_{it} + \lambda_{t} + u_{it}$$
El intercepto en la ecuación anterior se puede considerar como el “efecto” en $Y$ del año $t$ (o, más generalmente, período de tiempo $t$), por lo que los términos $\lambda_{1},…, \lambda_{T}$ se conocen como efectos fijos temporales. En algunas aplicaciones es útil considerar tanto efectos temporales fijos como efectos fijos de las entidades, el modelo se puede extender a: $$\begin{array}{c} \begin{aligned} Y_{it}&=\beta_{0} + \beta_{1}X_{it} + \gamma_{2}D2_{i} + … + \gamma_{n}Dn_{i} \ &+ \delta_{2}B2_{t} + … + \delta_{T}BT_{t} + u_{it} \end{aligned} \end{array} $$
Donde $\beta_{0}, \beta_{1}, \gamma_{2},…, \gamma_{n}$ y $\delta_{2},…, \delta_{T}$ son coeficientes desconocidos.
De forma general, el modelo anterior se puede escribir como: $$Y_{it}= \beta_{1}X_{it} + \alpha_{i} + \lambda_{t} + u_{it}$$
Donde $\alpha_{i}$ es el efecto fijo de la entidad y $\lambda_i$ es el efecto fijo temporal.
Aplicación
Volviendo al ejemplo anterior, el modelo poblacional con efectos fijos y efectos fijos temporales quedaría como: $$FatalityRate_{it} = \beta_1 BeerTax_{it} + StateEffects + TimeFixedEffects + u_{it}$$
Este modelo puede ser implementado tanto utilizando la función lm() o plm().
En el caso de la función lm(), solo tenemos que adicionar en la fórmula el regresor adicional del tiempo, year.
En el caso de la función plm(), simplemente se incluye el argumento effect = "twoways", para incluir tanto las dummies de entidad y las dummies temporales.
Para la implementación con lm:
fatal_tefe_lm_mod <- lm(fatal_rate ~ beertax + state + year - 1, data = Fatalities)
modelsummary::modelsummary(fatal_tefe_lm_mod,
gof_map = c("nobs","r.squared"),
output = "markdown")
| Model 1 | |
|---|---|
| beertax | -0.640 |
| (0.197) | |
| stateal | 3.511 |
| (0.333) | |
| stateaz | 2.965 |
| (0.099) | |
| statear | 2.873 |
| (0.142) | |
| stateca | 2.026 |
| (0.079) | |
| stateco | 2.050 |
| (0.086) | |
| statect | 1.671 |
| (0.090) | |
| statede | 2.227 |
| (0.083) | |
| statefl | 3.251 |
| (0.236) | |
| statega | 4.023 |
| (0.491) | |
| stateid | 2.862 |
| (0.106) | |
| stateil | 1.573 |
| (0.084) | |
| statein | 2.071 |
| (0.095) | |
| stateia | 1.987 |
| (0.110) | |
| stateks | 2.307 |
| (0.117) | |
| stateky | 2.317 |
| (0.086) | |
| statela | 2.678 |
| (0.174) | |
| stateme | 2.417 |
| (0.171) | |
| statemd | 1.827 |
| (0.088) | |
| statema | 1.423 |
| (0.093) | |
| statemi | 2.045 |
| (0.125) | |
| statemn | 1.635 |
| (0.101) | |
| statems | 3.491 |
| (0.223) | |
| statemo | 2.236 |
| (0.099) | |
| statemt | 3.172 |
| (0.101) | |
| statene | 2.008 |
| (0.113) | |
| statenv | 2.933 |
| (0.087) | |
| statenh | 2.272 |
| (0.151) | |
| statenj | 1.430 |
| (0.078) | |
| statenm | 3.957 |
| (0.109) | |
| stateny | 1.348 |
| (0.081) | |
| statenc | 3.226 |
| (0.268) | |
| statend | 1.908 |
| (0.109) | |
| stateoh | 1.857 |
| (0.109) | |
| stateok | 2.978 |
| (0.197) | |
| stateor | 2.366 |
| (0.087) | |
| statepa | 1.766 |
| (0.093) | |
| stateri | 1.270 |
| (0.083) | |
| statesc | 4.065 |
| (0.376) | |
| statesd | 2.523 |
| (0.151) | |
| statetn | 2.657 |
| (0.098) | |
| statetx | 2.613 |
| (0.117) | |
| stateut | 2.362 |
| (0.165) | |
| statevt | 2.561 |
| (0.150) | |
| stateva | 2.236 |
| (0.157) | |
| statewa | 1.874 |
| (0.088) | |
| statewv | 2.634 |
| (0.116) | |
| statewi | 1.775 |
| (0.083) | |
| statewy | 3.308 |
| (0.076) | |
| year1983 | -0.080 |
| (0.038) | |
| year1984 | -0.072 |
| (0.038) | |
| year1985 | -0.124 |
| (0.038) | |
| year1986 | -0.038 |
| (0.039) | |
| year1987 | -0.051 |
| (0.039) | |
| year1988 | -0.052 |
| (0.040) | |
| Num.Obs. | 336 |
| R2 | 0.993 |
Donde nótese se quita un año para no incurrir en multicolinealidad perfecta.
Recordando, la función lm() convierte automáticamente las variables factor. Básicamente, utilizando esta función estamos estimando $n+(T-1) = 48+6 = 54$ variables binarias.
Utilizando plm::plm():
fatal_tefe_mod <- plm(fatal_rate ~ beertax,
data = Fatalities,
index = c("state", "year"),
model = "within",
effect = "twoways")
modelsummary::modelsummary(fatal_tefe_mod,
vcov = vcovHC,
gof_map = c("nobs","r.squared"),
output = "markdown")
| Model 1 | |
|---|---|
| beertax | -0.640 |
| (0.350) | |
| Num.Obs. | 336 |
| R2 | 0.036 |
En el caso de plm::plm() solo se reporta el coeficiente estimado sobre $BeerTax$.
La función de regresión estimada es: $$\begin{aligned} \widehat{FatalityRate} = -\underset{(0.35)}{0.64} \times BeerTax + StateEffects + TimeFixedEffects \end{aligned}$$
¿Cómo se interpreta?
Un modelo general
Existen dos grandes fuentes de variables omitidas que no son tomadas en cuenta en ninguno de los modelos que hemos estimado hasta ahora: 1. Variables macroeconómicas 1. Leyes de tránsito
Estas variables podrían ser importantes para explicar el número de muertes por accidentes de tránsito.
Si se mira con detenimiento, Fatalities tiene información sobre las leyes específicas respecto a la edad para consumir bebidas alcohólicas en cada estado,drinkage, castigos para los infractores como jail y service, algunos indicadores macro como la tasa de desempleo, unemp o el ingreso per cápita, income.
Las variables que se utilizarán son las siguientes:
unemp: una variable numérica que indica la tasa de desempleo específica de cada estado.log(income): el logaritmo del ingreso real per cápita (en precios de 1988).miles: el promedio estatal de millas por conductor.drinkage: edad mínima legal para beber en cada estado.drinkagc: una versión discreta dedrinkageque clasifica los estados en cuatro categorías según la de edad mínima para beber; $18, 19, 20, 21$ y mayores. $\mathrm{R}$ denota esto como $[18,19), [19,20), [20,21)$ y $[21,22]$. Estas categorías se incluyen como regresores ficticios donde se elige $[21,22]$ como categoría de referencia.punish: una variable dummy con niveles si y no que mide si conducir en estado de ebriedad es severamente castigado con encarcelamiento obligatorio o servicio comunitario obligatorio (primera condena)
# Hacer discreto la edad lega mínima para beber
Fatalities$drinkagec <- cut(Fatalities$drinkage,
breaks = 18:22,
include.lowest = TRUE,
right = FALSE)
# Colocar la edad minima para beber [21, 22] como el nivel "base"
Fatalities$drinkagec <- relevel(Fatalities$drinkagec, "[21,22]")
# Cárcel obligatoria o servicio comunitario?
Fatalities$punish <- with(Fatalities, factor(jail == "yes" | service == "yes",
labels = c("no", "yes")))
# Conjunto de observaciones de todas las variables solo para 1982 y 1988
Fatalities_1982_1988 <- Fatalities[with(Fatalities, year == 1982 | year == 1988), ]
Ahora, se van a estimar $7$ modelos distintos (diferentes especificaciones utilizando plm::plm()
fatalities_mod1 <- lm(fatal_rate ~ beertax, data = Fatalities)
fatalities_mod2 <- plm(fatal_rate ~ beertax + state, data = Fatalities)
fatalities_mod3 <- plm(fatal_rate ~ beertax + state + year,
index = c("state","year"),
model = "within",
effect = "twoways",
data = Fatalities)
fatalities_mod4 <- plm(fatal_rate ~ beertax + state + year + drinkagec
+ punish + miles + unemp + log(income),
index = c("state", "year"),
model = "within",
effect = "twoways",
data = Fatalities)
fatalities_mod5 <- plm(fatal_rate ~ beertax + state + year + drinkagec
+ punish + miles,
index = c("state", "year"),
model = "within",
effect = "twoways",
data = Fatalities)
fatalities_mod6 <- plm(fatal_rate ~ beertax + year + drinkagec
+ punish + miles + unemp + log(income),
index = c("state", "year"),
model = "within",
effect = "twoways",
data = Fatalities)
fatalities_mod7 <- plm(fatal_rate ~ beertax + state + year + drinkagec
+ punish + miles + unemp + log(income),
index = c("state", "year"),
model = "within",
effect = "twoways",
data = Fatalities_1982_1988)
Además, para presentar los resultados, se utilizará la librería modelsummary utilizando los errores estándar robustos del tipo HC.
Finalmente, se genera la tabla de resultados:
models = list("OLS 1" = fatalities_mod1,
"Panel 1" = fatalities_mod2,
"Panel 2" = fatalities_mod3,
"Panel 3" = fatalities_mod4,
"Panel 4" = fatalities_mod5,
"Panel 5" = fatalities_mod6,
"Panel 6" = fatalities_mod7)
modelsummary::modelsummary(models,
gof_map = c("nobs", "r.squared"),
vcov = sandwich::vcovHC,
estimate = "{estimate}{stars}",
output="markdown")
| OLS 1 | Panel 1 | Panel 2 | Panel 3 | Panel 4 | Panel 5 | Panel 6 | |
|---|---|---|---|---|---|---|---|
| (Intercept) | 1.853*** | ||||||
| (0.047) | |||||||
| beertax | 0.365*** | -0.656* | -0.640+ | -0.445 | -0.690* | -0.445 | -0.926** |
| (0.054) | (0.288) | (0.350) | (0.288) | (0.342) | (0.288) | (0.322) | |
| drinkagec[18,19) | 0.028 | -0.010 | 0.028 | 0.037 | |||
| (0.068) | (0.080) | (0.068) | (0.096) | ||||
| drinkagec[19,20) | -0.018 | -0.076 | -0.018 | -0.065 | |||
| (0.048) | (0.066) | (0.048) | (0.093) | ||||
| drinkagec[20,21) | 0.032 | -0.100+ | 0.032 | -0.113 | |||
| (0.049) | (0.054) | (0.049) | (0.118) | ||||
| punishyes | 0.038 | 0.085 | 0.038 | 0.089 | |||
| (0.100) | (0.108) | (0.100) | (0.154) | ||||
| miles | 0.000 | 0.000+ | 0.000 | 0.000* | |||
| (0.000) | (0.000) | (0.000) | (0.000) | ||||
| unemp | -0.063*** | -0.063*** | -0.091*** | ||||
| (0.013) | (0.013) | (0.020) | |||||
| log(income) | 1.816** | 1.816** | 0.996 | ||||
| (0.616) | (0.616) | (0.637) | |||||
| Num.Obs. | 336 | 336 | 336 | 335 | 335 | 335 | 95 |
| R2 | 0.093 | 0.041 | 0.036 | 0.360 | 0.066 | 0.360 | 0.659 |
¿Cómo se interpreta?