DatasauRus
El objetivo de esta notebook es el de familiarizarnos con el uso de algunas técnicas estadísticas comunes y su uso (y su mis-use) en el análisis de datos.
En tal sentido, para la primera parte se utilizarán las librerías contenidas en el ecosistema de tidyverse, tales como dplyr para “arreglar” los datos o ggplot, para visualizarlos.
Configuraciones previas
Inicialmente,si es la primera vez que se usan, se deben instalar las librerías llamadas a continuación con la función install.packages():
install.packages("datasauRus")
install.packages("haven",dependencies = T)
install.packages("splitstackshape",dependencies = T)
library(tidyverse)
library(datasauRus)
library(haven)
library(splitstackshape)
Una vez instalada la librería, se puede llamar a las funciones que contiene de dos formas: tal como se ejecutó en la celda anterior, (utilizando la función library()) o, alternativamente, colocando el nombre de la librería seguido de un doble dos puntos ::, por ejemplo, dplyr::mutate(). En caso de que se elija la segunda opción no es necesario llamar a library, siempre y cuando se la tenga instalada en el equipo.
Es una buena práctica, especialmente cuando uno inicia, seguir el segundo método, aún cuando se llame a library() para que nuestro yo futuro recuerde de dónde sacó una determinada función.
Los datos
Todo análisis debe iniciarse cargando la materia prima del mismo: los datos. Ya sea desde un archivo plano (.csv, .txt,etc), desde diferentes instancias de base de datos relacionales (SQL Server, Oracle, etc.) o desde páginas de internet (urls, web scrapping, etc), el primer paso es lograr que R “lea” la información.
En este sentido, se utilizará una tabla de información contenida en la librería datasauRus:
data <- datasauRus::datasaurus_dozen
Como primer paso, se debe conocer el conjunto de datos.
head(data,10)
## # A tibble: 10 x 3
## dataset x y
## <chr> <dbl> <dbl>
## 1 dino 55.4 97.2
## 2 dino 51.5 96.0
## 3 dino 46.2 94.5
## 4 dino 42.8 91.4
## 5 dino 40.8 88.3
## 6 dino 38.7 84.9
## 7 dino 35.6 79.9
## 8 dino 33.1 77.6
## 9 dino 29.0 74.5
## 10 dino 26.2 71.4
O, viendo el final:
tail(data)
## # A tibble: 6 x 3
## dataset x y
## <chr> <dbl> <dbl>
## 1 wide_lines 34.7 19.6
## 2 wide_lines 33.7 26.1
## 3 wide_lines 75.6 37.1
## 4 wide_lines 40.6 89.1
## 5 wide_lines 39.1 96.5
## 6 wide_lines 34.6 89.6
Viendo la estructura del conjunto de datos:
dplyr::glimpse(data)
## Rows: 1,846
## Columns: 3
## $ dataset <chr> "dino", "dino", "dino", "dino", "dino", "dino", "dino", "dino"~
## $ x <dbl> 55.3846, 51.5385, 46.1538, 42.8205, 40.7692, 38.7179, 35.6410,~
## $ y <dbl> 97.1795, 96.0256, 94.4872, 91.4103, 88.3333, 84.8718, 79.8718,~
Como se puede observar, existen tres variables, $dataset$, una variable de texto o character y las variables $x$ e $y$, ambas numéricas.
Para entender la información, verificamos cuántas categorías existen en la variable $dataset$:
unique(data$dataset)
## [1] "dino" "away" "h_lines" "v_lines" "x_shape"
## [6] "star" "high_lines" "dots" "circle" "bullseye"
## [11] "slant_up" "slant_down" "wide_lines"
Como muestra, vamos a analizar $4$ variables tomadas al azar para realizar nuestro análisis de forma inicial:
set.seed(12)
unique(data$dataset)[runif(n = 4,min=1, max=length(unique(data$dataset)))]
## [1] "dino" "bullseye" "slant_down" "v_lines"
Dino
Inicialmente, vamos a realizar un subset de datos para quedarnos con dino.
Esto puede lograrse de varias formas, en este caso se ilustra con funciones de R base como con funciones obtenidas de dyplr:
dino <- data[data$dataset=="dino",]
head(dino,3)
## # A tibble: 3 x 3
## dataset x y
## <chr> <dbl> <dbl>
## 1 dino 55.4 97.2
## 2 dino 51.5 96.0
## 3 dino 46.2 94.5
O, viendo el final:
tail(dino,3)
## # A tibble: 3 x 3
## dataset x y
## <chr> <dbl> <dbl>
## 1 dino 50 95.8
## 2 dino 47.9 95
## 3 dino 44.1 92.7
Utilizando dplyr:
dino_dyplr <- data %>%
filter(dataset=="dino")
head(dino_dyplr)
## # A tibble: 6 x 3
## dataset x y
## <chr> <dbl> <dbl>
## 1 dino 55.4 97.2
## 2 dino 51.5 96.0
## 3 dino 46.2 94.5
## 4 dino 42.8 91.4
## 5 dino 40.8 88.3
## 6 dino 38.7 84.9
La media
dino está compuesto por dos variables continuas. Para calcular sus medias ocupamos la función mean():
mean(dino$x)
## [1] 54.26327
mean(dino$y)
## [1] 47.83225
Podemos redondear usando la función round()
round(mean(dino$x),digits = 2)
## [1] 54.26
round(mean(dino$y),digits = 2)
## [1] 47.83
Varianza - Desviación estándar
La varianza la obtenemos utilizando la función var():
var(dino$x)
## [1] 281.07
var(dino$y)
## [1] 725.516
La desviación estándar, la raiz cuadrada de la varianza, mediante sd():
sd(dino$x)
## [1] 16.76514
sd(dino$y)
## [1] 26.9354
Covarianza y correlación
Como se vio, una medida del tipo de relación lineal entre dos variables es la covarianza, la cual puede calcularse utilizando la función cov():
cov(dino$x,dino$y)
## [1] -29.11393
De esto, se deriva que la relación es negativa, es decir, cuando $x$ está por encima de su promedio, $y$ suele estar por debajo del suyo.
Complementando, para tener una idea de la magnitud de la relación, se calcula la correlación utilizando cor():
cor(dino$x, dino$y)
## [1] -0.06447185
El cual sugiere una leve relación negativa.
Rango
Se suele calcular el rango, la diferencia entre el valor máximo y el valor mínimo de los datos, para enteder la dispersión entre los mismos:
El valor mínimo se lo obtiene mediante la función min():
min(dino$x)
## [1] 22.3077
min(dino$y)
## [1] 2.9487
El valor máximo, mediante max():
max(dino$x)
## [1] 98.2051
max(dino$y)
## [1] 99.4872
Una forma alternativa
Si tenemos una rutina preestablecida (repetitiva) no hay necesidad de realizar el análisis muchas veces, sino que es posible crear un loop y ‘automatizar’ el análisis. Esto puede lograrse como se explica a continuación:
En primer lugar, obtenemos algunos datos sobre los cuales iterar (los mismos que íbamos a analizar anteriormente) y los añadimos al vector $prueba$:
set.seed(12)
prueba <- unique(data$dataset)[runif(n = 4,min=1, max=length(unique(data$dataset)))]
prueba
## [1] "dino" "bullseye" "slant_down" "v_lines"
Los loops en R tienen la siguiente estructura:
## for(iterador in lista){
##
## hacer algo
##
## }
Por ejemplo:
for(i in c("a","c","d")){
print(i)
}
## [1] "a"
## [1] "c"
## [1] "d"
Ahora, verificando los nombres de las columnas:
colnames(data)
## [1] "dataset" "x" "y"
Verificando los valures únicos de la columna dataset:
unique(data$dataset)
## [1] "dino" "away" "h_lines" "v_lines" "x_shape"
## [6] "star" "high_lines" "dots" "circle" "bullseye"
## [11] "slant_up" "slant_down" "wide_lines"
for(i in unique(data$dataset)){
print(paste("Dataset",i,sep=" "))
datos <- data[data$dataset==paste(i),]
cat(paste("Media x:", round(mean(datos$x),2),sep=" "),"\n")
cat(paste("Media y:", round(mean(datos$y),2),sep=" "),"\n")
cat(paste("Varianza x:", round(var(datos$x),2)),"\n")
cat(paste("Varianza y:", round(var(datos$y),2)),"\n")
cat(paste("Desv. Estd. x:", round(sd(datos$x),2)),"\n")
cat(paste("Desv. Estd. y:", round(sd(datos$y),2)),"\n")
cat(paste("Covarianza:", round(cov(datos$x,datos$y),2)),"\n")
cat(paste("Correlación:", round(cor(datos$x,datos$y),2)),"\n")
cat("\n")
}
## [1] "Dataset dino"
## Media x: 54.26
## Media y: 47.83
## Varianza x: 281.07
## Varianza y: 725.52
## Desv. Estd. x: 16.77
## Desv. Estd. y: 26.94
## Covarianza: -29.11
## Correlación: -0.06
##
## [1] "Dataset away"
## Media x: 54.27
## Media y: 47.83
## Varianza x: 281.23
## Varianza y: 725.75
## Desv. Estd. x: 16.77
## Desv. Estd. y: 26.94
## Covarianza: -28.97
## Correlación: -0.06
##
## [1] "Dataset h_lines"
## Media x: 54.26
## Media y: 47.83
## Varianza x: 281.1
## Varianza y: 725.76
## Desv. Estd. x: 16.77
## Desv. Estd. y: 26.94
## Covarianza: -27.87
## Correlación: -0.06
##
## [1] "Dataset v_lines"
## Media x: 54.27
## Media y: 47.84
## Varianza x: 281.23
## Varianza y: 725.64
## Desv. Estd. x: 16.77
## Desv. Estd. y: 26.94
## Covarianza: -31.37
## Correlación: -0.07
##
## [1] "Dataset x_shape"
## Media x: 54.26
## Media y: 47.84
## Varianza x: 281.23
## Varianza y: 725.22
## Desv. Estd. x: 16.77
## Desv. Estd. y: 26.93
## Covarianza: -29.62
## Correlación: -0.07
##
## [1] "Dataset star"
## Media x: 54.27
## Media y: 47.84
## Varianza x: 281.2
## Varianza y: 725.24
## Desv. Estd. x: 16.77
## Desv. Estd. y: 26.93
## Covarianza: -28.43
## Correlación: -0.06
##
## [1] "Dataset high_lines"
## Media x: 54.27
## Media y: 47.84
## Varianza x: 281.12
## Varianza y: 725.76
## Desv. Estd. x: 16.77
## Desv. Estd. y: 26.94
## Covarianza: -30.94
## Correlación: -0.07
##
## [1] "Dataset dots"
## Media x: 54.26
## Media y: 47.84
## Varianza x: 281.16
## Varianza y: 725.24
## Desv. Estd. x: 16.77
## Desv. Estd. y: 26.93
## Covarianza: -27.25
## Correlación: -0.06
##
## [1] "Dataset circle"
## Media x: 54.27
## Media y: 47.84
## Varianza x: 280.9
## Varianza y: 725.23
## Desv. Estd. x: 16.76
## Desv. Estd. y: 26.93
## Covarianza: -30.85
## Correlación: -0.07
##
## [1] "Dataset bullseye"
## Media x: 54.27
## Media y: 47.83
## Varianza x: 281.21
## Varianza y: 725.53
## Desv. Estd. x: 16.77
## Desv. Estd. y: 26.94
## Covarianza: -30.98
## Correlación: -0.07
##
## [1] "Dataset slant_up"
## Media x: 54.27
## Media y: 47.83
## Varianza x: 281.19
## Varianza y: 725.69
## Desv. Estd. x: 16.77
## Desv. Estd. y: 26.94
## Covarianza: -30.99
## Correlación: -0.07
##
## [1] "Dataset slant_down"
## Media x: 54.27
## Media y: 47.84
## Varianza x: 281.12
## Varianza y: 725.55
## Desv. Estd. x: 16.77
## Desv. Estd. y: 26.94
## Covarianza: -31.15
## Correlación: -0.07
##
## [1] "Dataset wide_lines"
## Media x: 54.27
## Media y: 47.83
## Varianza x: 281.23
## Varianza y: 725.65
## Desv. Estd. x: 16.77
## Desv. Estd. y: 26.94
## Covarianza: -30.08
## Correlación: -0.07
Como se observa, los loops también pueden volverse complicados, aún más si hubiésemos tenido que almacenar los resultados en alguna estructura compacta.
Se debe notar, sin embargo, algo sorprendente: aún cuando los $datasets$ son distintos, los principales estadísticos son iguales.
Otra alternativa: the “tidy way”
Una forma más sencilla de obtener los mismos resultados, hubiese sido aprovechando algunas funciones diseñadas para esto. Así, dplyr contiene algunas funciones importantes:
data_sum = data %>%
group_by(dataset) %>%
summarize(
media_x = round(mean(x),2),
media_y = round(mean(y),2),
var_x = round(var(x),2),
var_y = round(var(y),2),
esv_est_x = round(sd(x),2),
desv_est_y = round(sd(y),2),
cov_x_y = round(cov(x,y),2),
corr_x_y = round(cor(x, y),2)
)
Visualizando los resultados:
head(data_sum)
## # A tibble: 6 x 9
## dataset media_x media_y var_x var_y esv_est_x desv_est_y cov_x_y corr_x_y
## <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 away 54.3 47.8 281. 726. 16.8 26.9 -29.0 -0.06
## 2 bullseye 54.3 47.8 281. 726. 16.8 26.9 -31.0 -0.07
## 3 circle 54.3 47.8 281. 725. 16.8 26.9 -30.8 -0.07
## 4 dino 54.3 47.8 281. 726. 16.8 26.9 -29.1 -0.06
## 5 dots 54.3 47.8 281. 725. 16.8 26.9 -27.2 -0.06
## 6 h_lines 54.3 47.8 281. 726. 16.8 26.9 -27.9 -0.06
Si observamos, el resultado es un tibble (algo muy parecido a un dataframe), el cual pudo haberse asignado a un nuevo objeto.
Por otra parte, queda una duda, ¿son todos estos $dataset$ iguales? Para quitarnos la duda, vamos a graficarlos utilizando ggplot():
Análisis Gráfico
¿Qué sucede si graficamos?
data %>%
filter(dataset %in% c("dino","circle","star"))%>%
ggplot(aes(x=x, y=y, colour=dataset))+
geom_point()+
theme_minimal()+
theme(legend.position = "none")+
facet_wrap(~dataset, ncol=3)
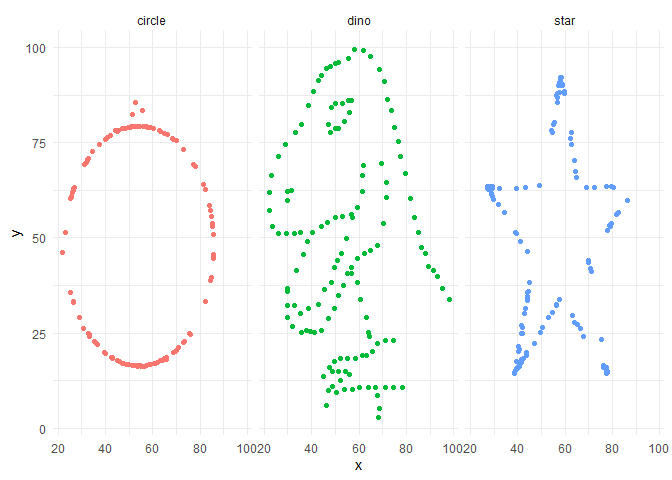
Como es evidente, los diferentes $dataset$ son distinto, sin embargo, producen los mismos resultados… ¿por qué?
Conclusión
Una imagen vale más que mil palabras. La importancia de “dibujar” los datos antes de realizar cualquier análisis numérico.