Medición del riesgo de crédito: Construcción de un Scorecard
Objetivo
Este documento tiene como objetivo ilustrar los pasos (simplificados) para la modelación de riesgo de crédito. Para esto se utilizará el conjunto de datos Credit Card Approval Prediction que contiene información sobre solicitudes de tarjetas de crédito y la evolución de las aprobadas.
Adicionalmente se utilizarán dos metodologías para medir la probabilidad de impago: Un modelo logit estándar y la metodología “scorecard” basada en el peso de la evidencia (en adelante WoE, por sus siglas en inglés).
Si bien el estudio no trata de ser extensivo (no se utilizarán todas las técnicas disponibles en cada una de las etapas), sí trata de dar una visión general del proceso de modelación y las técnicas antes mencionadas.
Metodología clásica
Setup
Inicialmente cargamos las librerías que se utilizarán en el análisis:
library(caret)
library(tidyverse)
library(scorecard)
library(ggcorrplot)
library(kableExtra)
Básicamente se utilizan las librerías caret especializada en modelos de machine learning, tidyverse para la limpieza y visualización de datos, scorecard para el cálculo rápido de los WoE y ggcorrplot un wrapper para la visualización de matrices de correlación.
Cargar y limpiar los datos
Como primer paso cargamos los datos:
application_record <- read.csv("3_Clasificacion/CreditCardApproval_Dataset/application_record.csv")
credit_record <- read.csv("3_Clasificacion/CreditCardApproval_Dataset/credit_record.csv")
Como contexto, el conjunto de datos application_record.csv almacena la información de las solicitudes por tarjetas de crédito y algunas características que fueron tomadas al momento de que el cliente hizo la solicitud. El detalle se explica en la siguiente tabla:
| Nombre de la variable | Detalle |
|---|---|
ID | Número de cliente |
CODE_GENDER | Género |
FLAG_OWN_CAR | ¿Tiene un auto? |
FLAG_OWN_REALTY | ¿Tiene algún inmueble? |
CNT_CHILDREN | Número de hijos |
AMT_INCOME_TOTAL | Ingreso anual |
NAME_INCOME_TYPE | Categoría del ingreso |
NAME_EDUCATION_TYPE | Nivel de educación |
NAME_FAMILY_STATUS | Estado civil |
NAME_HOUSING_TYPE | Tipo de domicilio |
DAYS_BIRTH | Edad en días contado hacia atrás desde el día 0 (-1 = Ayer) |
DAYS_EMPLOYED | Antigüedad laboral contado hacia atrás desde el día 0 ( 0 > es desempleado) |
FLAG_MOBIL | ¿Tiene teléfono móvil? |
FLAG_WORK_PHONE | ¿Tiene teléfono del trabajo |
FLAG_PHONE | ¿Tiene un teléfono fijo? |
FLAG_EMAIL | ¿Tiene correo electrónico? |
OCCUPATION_TYPE | Ocupación |
CNT_FAM_MEMBERS | Tamaño de la familia |
Por otra parte, credit_record.csv contiene el estado actual de los clientes a los cuales sí le fue aprobada la tarjeta de crédito:
| Nombre de la variable | Detalle |
|---|---|
ID | Número de cliente |
MONTHS_BALANCE | Mes en que se extrajo la información. (-1 es el mes pasado) |
STATUS | Estado del crédito (0: 1-29 de atraso; 1: 30-59 días de atraso; 2: 60-89 días de atraso; 3: 90-119 días de atraso; 4: 120-149 días de atraso; 5: Castigados por más de 150 días de atraso; C: Vigente; X: Sin crédito ese mes) |
Predictores
Inicialmente, verificamos el tipo de información que existe en application_record.csv:
application_record |>
head() |>
kable(format="markdown") |>
kable_styling("striped") |>
scroll_box(width = "100%")
| ID | CODE_GENDER | FLAG_OWN_CAR | FLAG_OWN_REALTY |
|---|---|---|---|
| 5008804 | M | Y | Y |
| 5008805 | M | Y | Y |
| 5008806 | M | Y | Y |
| 5008808 | F | N | Y |
| 5008809 | F | N | Y |
| 5008810 | F | N | Y |
Este conjunto de datos contiene $438,557$ observaciones de aplicaciones de tarjetas de crédito, una columna identificador, ID (primary key) y $17$ características que pueden ser utilizadas como predictores del impago.
Como se puede observar, existen variables numéricas y caracteres que no están en el formato correcto para realizar el análisis. Más adelante volveremos sobre ello.
Target
Ahora, analizando los datos contenidos en credit_record.csv:
credit_record |>
head() |>
kable(format="markdown") |>
kable_styling("striped") |>
scroll_box(width = "100%")
| ID | MONTHS_BALANCE | STATUS |
|---|---|---|
| 5001711 | 0 | X |
| 5001711 | -1 | 0 |
| 5001711 | -2 | 0 |
| 5001711 | -3 | 0 |
| 5001712 | 0 | C |
| 5001712 | -1 | C |
Nótese que este conjunto de datos contiene el historial de pagos de las tarjetas de crédito aprobadas, compuesto por el mes desde que se otorgó la tarjeta, MONTHS_BALANCE y el estado en que se encontraba esa tarjeta a fin de mes, STATUS, además de un identificador que las vincula con sus características, ID.
Este conjunto de datos tiene $1,048,575$ filas, un número muy superior a las solicitadas, lo cual nos da un indicio que tendremos que agregar esta información de alguna manera.
Entendiendo el target
Entender esta información es vital para nuestro análisis. Es decir, dado que el target es la variable que vamos a predecir, debemos tener un correcto entendimiento del mismo. Una primer pregunta es entender la cantidad de valores únicos:
credit_record |>
distinct(ID) |>
summarise(Count = n()) |>
kable(format="markdown") |>
kable_styling("striped") |>
scroll_box(width = "100%")
| Count |
|---|
| 45985 |
Es decir, a la fecha de extracción de los datos se tenían $45,985$ tarjetas colocadas. ¿Cómo se han ido aprobando en el tiempo?
credit_record |>
arrange(ID,MONTHS_BALANCE) |>
distinct(ID,.keep_all = T) |>
group_by(MONTHS_BALANCE) |>
summarise(Count = n()) |>
ggplot(aes(x= MONTHS_BALANCE, y=Count))+
geom_bar(stat= "identity", color ="black", fill = "steelblue") +
geom_text(aes(label= ifelse(-MONTHS_BALANCE %% 5 == 0,Count, NA)),
position = position_dodge(width = 1), vjust = -1.5, size = 2 ) +
labs( x= "\nMes de otorgación" ,y = "Número de nuevas tarjetas\n")+
theme_bw()
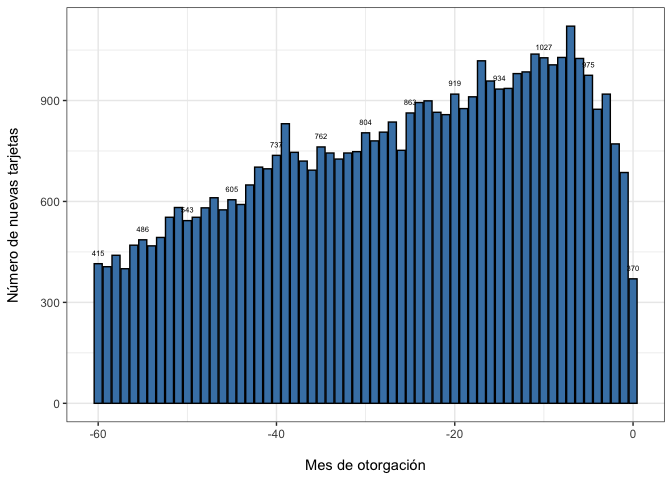
Nótese la tendencia positiva en la colocación de tarjetas.
Lo siguiente es tener una idea visual del rendimiento de esta cartera en términos de impago o del STATUS de las tarjetas en el tiempo. Como no se tiene una medida monetaria, que es usualmente la forma en que se reporta el impago, veremos qué proporción de las tarjetas colocadas se encuentran en los diferentes estados. Para esto, recordemos la definición de STATUS:
STATUS | Definición | Estado del crédito (reclasificación) |
|---|---|---|
| C | 0 días de atraso | Vigente |
| X | Sin crédito ese mes | Vigente |
| 0 | 1 a 29 días de atraso | Vigente |
| 1 | 30 a 59 días de atraso | Vencido |
| 2 | 60 a 89 días de atraso | Vencido |
| 3 | 90 a 119 días de atraso | Ejecución |
| 4 | 120-149 días de atraso | Ejecución |
| 5 | > 150 días de atraso | Castigado (según política) |
Graficando:
credit_record |>
mutate(Estado = case_when(STATUS== "0" |STATUS== "C" | STATUS=="X" ~ "Vigente",
STATUS== "1" |STATUS== "2" ~ "Vencido",
STATUS== "3" |STATUS== "4" ~ "Ejecución",
STATUS== "5" ~ "Castigado")) |>
group_by(MONTHS_BALANCE,Estado) |>
summarise(Count = n()) |>
ggplot(aes(x= MONTHS_BALANCE, y=Count, fill= Estado))+
geom_bar(stat= "identity", color ="black") +
labs( x= "\nMes" ,y = "Número de operaciones\n")+
scale_fill_manual(values = c("gray1","gray30", "gray60","steelblue"))+
theme_bw()
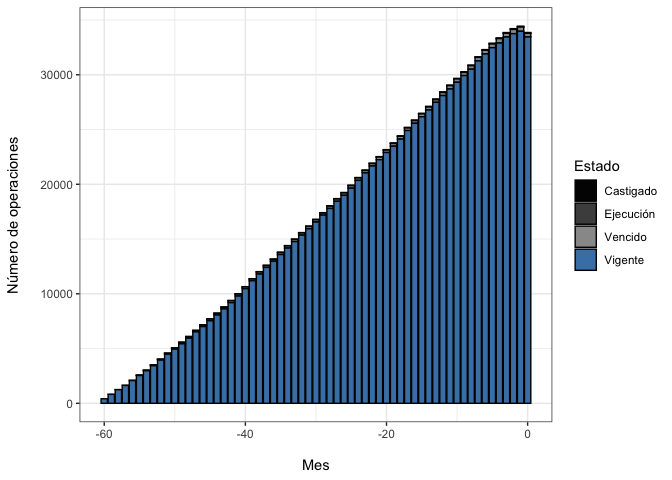
Nótese que aquí vemos una conducta importante: del total de las tarjetas otorgadas, solo una pequeña proporción se encuentra en algún estado que denote impago. Esta característica de los datos es conocida en la literatura como class imbalance y deberá ser tomada en cuenta a la hora de la modelación.
Viendo el estado como proporción:
credit_record |>
mutate(Estado = case_when(STATUS== "0" |STATUS== "C" | STATUS=="X" ~ "Vigente",
STATUS== "1" |STATUS== "2" ~ "Vencido",
STATUS== "3" |STATUS== "4" ~ "Ejecución",
STATUS== "5" ~ "Castigado")) |>
group_by(MONTHS_BALANCE,Estado) |>
summarise(Count = n()) |>
ggplot(aes(x= MONTHS_BALANCE, y=Count, fill= Estado))+
geom_bar(stat= "identity", color ="black", position = "fill") +
labs( x= "\nMes" ,y = "Proporción de operaciones\n")+
scale_fill_manual(values = c("gray1","gray30", "gray60","steelblue"))+
theme_bw()
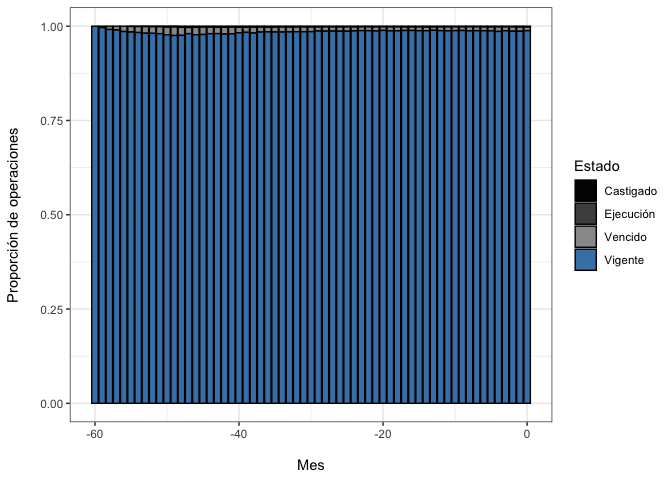
El gráfico anterior reafirma que la proporción de tarjetas que muestran algún indicio de impago es bastante pequeño. Es más, el mes de extracción de los datos solo el $1.19\%$ de las tarjetas mostraba un estado que no sea vigente.
Finalmente, para tener una idea de cómo ha evolucionado esta proporción en el tiempo, se grafica la proporción de operaciones “morosas” en el tiempo. Esto se define como1:
$$mora = \frac{Vencido+Ejecución+Castigado}{Vigente+Vencido+Ejecución+Castigado} $$
credit_record |>
mutate(Estado = case_when(STATUS== "0" |STATUS== "C" | STATUS=="X" ~ "Vigente",
STATUS== "1" |STATUS== "2" ~ "Vencido",
STATUS== "3" |STATUS== "4" ~ "Ejecución",
STATUS== "5" ~ "Castigado"),
Mora = ifelse(Estado != "Vigente", "Mora", "Vigente")) |>
group_by(MONTHS_BALANCE,Mora) |>
summarise(Count = n()) |>
# ungroup() |>
mutate(prop= Count/sum(Count)*100) |>
filter(Mora == "Mora") |>
ggplot(aes(x= MONTHS_BALANCE, y=prop))+
geom_bar(stat= "identity", color ="black", fill= "steelblue") +
geom_text(aes(label= ifelse(-MONTHS_BALANCE %% 4 == 0,round(prop,2), NA)),
position = position_dodge(width = 1), vjust = -2.5, size = 2.5 ) +
labs( x= "\nMes" ,y = "Proporción de tarjetas en mora\n")+
#scale_fill_manual(values = c("gray1","gray30", "gray60","steelblue"))+
theme_bw()
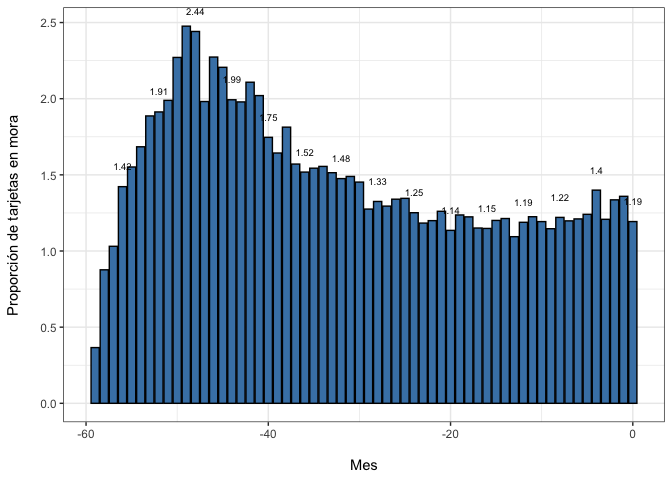
Donde se observa que la proporción de tarjetas en mora se ha mantenido en torno al $1.2\%$
Análisis de cohortes
Una cuestión interesante es ver cómo se comportaron, digamos los primeros 12 meses, las tarjetas que se otorgaron hace 60 meses y analizarlas como un segmento particular. Luego, podríamos preguntarnos lo mismo pero solamente con las tarjetas que se otorgaron hace 59 meses y hacia adelante. Este tipo de análisis suele llamarse de “cohortes” o “vintage” y nos permite comparar las operaciones en el mismo horizonte temporal. Esto va a ser importante cuando tengamos que elegir la definición de mora o target que vamos a intentar predecir.
cohort <- credit_record |>
arrange(ID,MONTHS_BALANCE,STATUS) %>%
group_by(ID) %>%
slice(1:24) %>%
mutate(Mes = seq(1:length(ID)),
Estado = case_when(STATUS== "0" |STATUS== "C" ~ "Vigente",
STATUS== "1" |STATUS== "2" ~ "Vencido",
STATUS== "3" |STATUS== "4" ~ "Ejecutado",
STATUS== "5" ~ "Castigado",
TRUE ~ "Vigente"),
Mora = ifelse(Estado %in% c("Vencido","Ejecutado","Castigado"),1,0))
cohort |>
group_by(ID) |>
mutate(Mes_inicial = first(MONTHS_BALANCE)) |>
group_by(Mes_inicial,Mes) |>
summarise(Mora = round(mean(Mora)*100,2 )) |>
#pivot_wider(names_from = Mes, values_from = Mora) |>
ggplot(aes(y= -Mes_inicial,x=Mes, fill=Mora))+
geom_tile()+
scale_fill_gradient(low="gray90", high="steelblue") +
labs(x = "\nMeses desde que se le otorgó la tarjeta",
y = "Hace cuántos meses se le otorgó la tarjeta\n")+
theme_minimal()
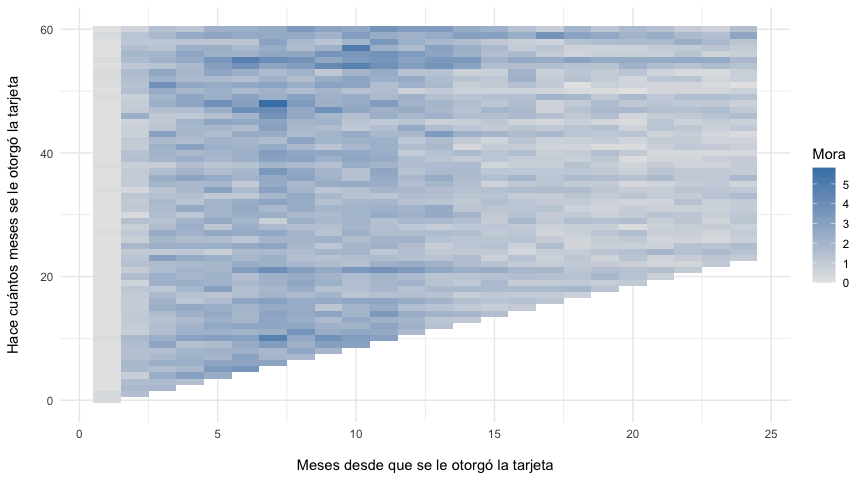
Nótese del gráfico anterior que parece haber un incremento en la morosidad entre los meses 4 a 12. Una vez pasado los 12 meses de otorgada la tarjeta los niveles de impago suelen disminuir. Esto puede tener distintas explicaciones, que van desde la política crediticia de la entidad, el mercado al que se está abordando, entre otros.
El análisis anterior es importante porque nos permite incluir la temporalidad en nuestro target, es decir, dado que un individuo que recibe una tarjeta de crédito hoy puede estar vigente el siguiente mes y el siguiente pero quizás no el tercero, debemos definir cuándo una tarjeta puede clasificarse como morosa, es decir, cuál es el horizonte temporal de nuestra predicción. Una primer opción sería:
Se define como morosa o delincuencial una tarjeta de crédito que en los primeros 12 meses de haber sido otorgada haya tenido 30 días o más de atraso en sus pagos.
Por tanto, para codificar nuestra variable $Y$ tenemos que ir tarjeta por tarjeta y, desde el momento de su otorgación hasta el mes $12$, verificar si cae dentro de nuestra definición de mora. El siguiente bloque de código hace precisamente eso:
# Crear un df con aquellas tarjetas con más de 12 meses de uso
cc_mt12m <- credit_record |>
arrange(ID,MONTHS_BALANCE) |>
distinct(ID,.keep_all = T) |>
filter(MONTHS_BALANCE <= -12) |>
select(ID)
# Filtrar en `credit_record.csv` aquellas tarjetas que tienen más de 12 meses y
# crear una variable mora que tome 1 si en cualquiera de estos meses se cumple
# nuestra definición de mora
target_mt12m <- credit_record |>
filter(ID %in% cc_mt12m$ID) |>
arrange(ID,MONTHS_BALANCE) |>
group_by(ID) |>
mutate(index = row_number()) |>
filter(index <= 12) |>
mutate(mora = ifelse(STATUS %in% c("1","2","3","4","5"), 1, 0))
target_30dpd_12m <- target_mt12m |>
group_by(ID) |>
summarise(mora = max(mora))
target_30dpd_12m |>
head(10) |>
kable(format="markdown") |>
kable_styling("striped") |>
scroll_box(width = "100%")
| ID | mora |
|---|---|
| 5001712 | 0 |
| 5001713 | 0 |
| 5001714 | 0 |
| 5001715 | 0 |
| 5001717 | 0 |
| 5001718 | 0 |
| 5001719 | 0 |
| 5001720 | 0 |
| 5001723 | 0 |
| 5001724 | 0 |
¿Cuántas tarjetas caen en nuestra definición?
prop_table <- prop.table(table(target_30dpd_12m$mora))*100
prop_table |>
head() |>
kable(format="markdown") |>
kable_styling("striped") |>
scroll_box(width = "100%")
| Mora | Freq |
|---|---|
| 0 | 89.91322 |
| 1 | 10.08678 |
Nótese que aproximadamente un $10\%$ de las tarjetas otorgadas cumplió presentó un atraso de al menos $30$ días los primeros $12$ meses después de otorgada.
Vamos a realizar el mismo ejercicio pero alargando el horizonte de predicción a $24$ meses:
# Crear un df con aquellas tarjetas con más de 24 meses de uso
cc_mt24m <- credit_record |>
arrange(ID,MONTHS_BALANCE) |>
distinct(ID,.keep_all = T) |>
filter(MONTHS_BALANCE <= -24) |>
select(ID)
# Filtrar en `credit_record.csv` aquellas tarjetas que tienen más de 12 meses y
# crear una variable mora que tome 1 si en cualquiera de estos meses se cumple
# nuestra definición de mora
target_mt24m <- credit_record |>
filter(ID %in% cc_mt24m$ID) |>
arrange(ID,MONTHS_BALANCE) |>
group_by(ID) |>
mutate(index = row_number()) |>
filter(index <= 24) |>
mutate(mora = ifelse(STATUS %in% c("1","2","3","4","5"), 1, 0))
target_30dpd_24m <- target_mt24m |>
group_by(ID) |>
summarise(mora = max(mora))
prop_table1 <- prop.table(table(target_30dpd_24m$mora))*100
prop_table1 |>
kable(format="markdown") |>
kable_styling("striped") |>
scroll_box(width = "100%")
| Mora | Freq |
|---|---|
| 0 | 87.80305 |
| 1 | 12.19695 |
Donde se incrementa la proporción de tarjetas que cumplen esta definición, pero se reduce el tamaño de la muestra, pues se deben omitir todas las tarjetas que no tengan al menos $24$ meses de antigüedad.
Así, para la modelación, se utilizará la primer definición que se reproduce a continuación:
Se define como morosa o delincuencial una tarjeta de crédito que en los primeros 12 meses de haber sido otorgada haya tenido 30 días o más de atraso en sus pagos.
Finalmente, convertimos el target en un factor:
target_30dpd_12m$mora <- as.factor(ifelse(target_30dpd_12m$mora==1,"Yes","No"))
Feature engineering
Ahora vamos a analizar la información contenida en application_record.csv y la vamos a transformar de modo que se puedan utilizar luego como inputs en el modelo.
application_record |>
head() |>
kable(format="markdown") |>
kable_styling("striped") |>
scroll_box(width = "100%")
| ID | CODE_GENDER | FLAG_OWN_CAR | FLAG_OWN_REALTY |
|---|---|---|---|
| 5008804 | M | Y | Y |
| 5008805 | M | Y | Y |
| 5008806 | M | Y | Y |
| 5008808 | F | N | Y |
| 5008809 | F | N | Y |
| 5008810 | F | N | Y |
Missing values
Primero, verificamos que no hayan missing values:
NAs <- sapply(application_record, function(x) sum(is.na(x)))
NULLs <- sapply(application_record, function(x) sum(is.null(x)))
Blank <- sapply(application_record, function(x) sum(ifelse(x=="",1,0)))
data.frame(NAs,NULLs,Blank) |>
kable(format="markdown") |>
kable_styling("striped") |>
scroll_box(width = "100%")
| Variable | NAs | NULLs | Blank |
|---|---|---|---|
| ID | 0 | 0 | 0 |
| CODE_GENDER | 0 | 0 | 0 |
| FLAG_OWN_CAR | 0 | 0 | 0 |
| FLAG_OWN_REALTY | 0 | 0 | 0 |
| CNT_CHILDREN | 0 | 0 | 0 |
| AMT_INCOME_TOTAL | 0 | 0 | 0 |
| NAME_INCOME_TYPE | 0 | 0 | 0 |
| NAME_EDUCATION_TYPE | 0 | 0 | 0 |
| NAME_FAMILY_STATUS | 0 | 0 | 0 |
| NAME_HOUSING_TYPE | 0 | 0 | 0 |
| DAYS_BIRTH | 0 | 0 | 0 |
| DAYS_EMPLOYED | 0 | 0 | 0 |
| FLAG_MOBIL | 0 | 0 | 0 |
| FLAG_WORK_PHONE | 0 | 0 | 0 |
| FLAG_PHONE | 0 | 0 | 0 |
| FLAG_EMAIL | 0 | 0 | 0 |
| OCCUPATION_TYPE | 0 | 0 | 134203 |
| CNT_FAM_MEMBERS | 0 | 0 | 0 |
La variable OCCUPATION_TYPE contiene un gran número de variables faltantes. Sin embargo, esto también pueden ocurrir porque son individuos que están desempleados:
# Crear un df con una variable indicador para el empleo
data_tmp <- application_record |>
mutate(Employment=ifelse(DAYS_EMPLOYED > 0,0,1)) |>
select(Employment, OCCUPATION_TYPE)
# Obtener las proporción de individuos empleados y desempleados
prop.table(table(data_tmp$Employment)) |>
kable(format="markdown") |>
kable_styling("striped") |>
scroll_box(width = "100%")
| Employment | Freq |
|---|---|
| 0 | 0.1717656 |
| 1 | 0.8282344 |
prop.table(table(data_tmp$Employment, data_tmp$OCCUPATION_TYPE)) |>
kable(format="markdown") |>
kable_styling("striped") |>
scroll_box(width = "100%")
| Accountants | Cleaning staff | Cooking staff | Core staff | Drivers | High skill tech staff | HR staff | IT staff | Laborers | Low-skill Laborers | Managers | Medicine staff | Private service staff | Realty agents | Sales staff | Secretaries | Security staff | Waiters/barmen staff | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.1717656 | 0.0000000 | 0.0000000 | 0.0000000 | 0.0000000 | 0.0000000 | 0.0000000 | 0.0000000 | 0.0000000 | 0.0000000 | 0.0000000 | 0.0000000 | 0.0000000 | 0.0000000 | 0.0000000 | 0.0000000 | 0.0000000 | 0.0000000 | 0.0000000 |
| 1 | 0.1342448 | 0.0364491 | 0.0133278 | 0.0184149 | 0.0980648 | 0.0594906 | 0.0394225 | 0.0017649 | 0.0013772 | 0.1784033 | 0.0048796 | 0.0809176 | 0.0308284 | 0.0078804 | 0.0023737 | 0.0937119 | 0.0046607 | 0.0182257 | 0.0037965 |
Como se puede observar, existe un $13.4\%$ de los individuos empleados que no tiene un OCCUPATION_TYPE por lo cual se eliminará esta variable del análisis2:
application_record$OCCUPATION_TYPE <- NULL
Factors for analysis
Básicamente, en este modelo tenemos variables indicadores (que toman solo 2 valores), variables categóricas (múltiples valores) y variables numéricas.
application_record |>
head() |>
kable(format="markdown") |>
kable_styling("striped") |>
scroll_box(width = "100%")
| ID | CODE_GENDER | FLAG_OWN_CAR | FLAG_OWN_REALTY | CNT_CHILDREN | AMT_INCOME_TOTAL | NAME_INCOME_TYPE | NAME_EDUCATION_TYPE | NAME_FAMILY_STATUS | NAME_HOUSING_TYPE | DAYS_BIRTH | DAYS_EMPLOYED | FLAG_MOBIL | FLAG_WORK_PHONE | FLAG_PHONE | FLAG_EMAIL | CNT_FAM_MEMBERS |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 5008804 | M | Y | Y | 0 | 427500 | Working | Higher education | Civil marriage | Rented apartment | -12005 | -4542 | 1 | 1 | 0 | 0 | 2 |
| 5008805 | M | Y | Y | 0 | 427500 | Working | Higher education | Civil marriage | Rented apartment | -12005 | -4542 | 1 | 1 | 0 | 0 | 2 |
| 5008806 | M | Y | Y | 0 | 112500 | Working | Secondary / secondary special | Married | House / apartment | -21474 | -1134 | 1 | 0 | 0 | 0 | 2 |
| 5008808 | F | N | Y | 0 | 270000 | Commercial associate | Secondary / secondary special | Single / not married | House / apartment | -19110 | -3051 | 1 | 0 | 1 | 1 | 1 |
| 5008809 | F | N | Y | 0 | 270000 | Commercial associate | Secondary / secondary special | Single / not married | House / apartment | -19110 | -3051 | 1 | 0 | 1 | 1 | 1 |
| 5008810 | F | N | Y | 0 | 270000 | Commercial associate | Secondary / secondary special | Single / not married | House / apartment | -19110 | -3051 | 1 | 0 | 1 | 1 | 1 |
fct_var <- c("CODE_GENDER","FLAG_OWN_CAR","FLAG_OWN_REALTY","NAME_INCOME_TYPE","NAME_EDUCATION_TYPE","NAME_FAMILY_STATUS","NAME_HOUSING_TYPE","FLAG_MOBIL","FLAG_WORK_PHONE","FLAG_PHONE","FLAG_EMAIL")
application_record <- application_record |>
mutate_at(fct_var, as.factor)
Revisando el conjunto de datos:
application_record |>
head() |>
kable(format="markdown") |>
kable_styling("striped") |>
scroll_box(width = "100%")
| ID | CODE_GENDER | FLAG_OWN_CAR | FLAG_OWN_REALTY | CNT_CHILDREN | AMT_INCOME_TOTAL | NAME_INCOME_TYPE | NAME_EDUCATION_TYPE | NAME_FAMILY_STATUS | NAME_HOUSING_TYPE | DAYS_BIRTH | DAYS_EMPLOYED | FLAG_MOBIL | FLAG_WORK_PHONE | FLAG_PHONE | FLAG_EMAIL | CNT_FAM_MEMBERS |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 5008804 | M | Y | Y | 0 | 427500 | Working | Higher education | Civil marriage | Rented apartment | -12005 | -4542 | 1 | 1 | 0 | 0 | 2 |
| 5008805 | M | Y | Y | 0 | 427500 | Working | Higher education | Civil marriage | Rented apartment | -12005 | -4542 | 1 | 1 | 0 | 0 | 2 |
| 5008806 | M | Y | Y | 0 | 112500 | Working | Secondary / secondary special | Married | House / apartment | -21474 | -1134 | 1 | 0 | 0 | 0 | 2 |
| 5008808 | F | N | Y | 0 | 270000 | Commercial associate | Secondary / secondary special | Single / not married | House / apartment | -19110 | -3051 | 1 | 0 | 1 | 1 | 1 |
| 5008809 | F | N | Y | 0 | 270000 | Commercial associate | Secondary / secondary special | Single / not married | House / apartment | -19110 | -3051 | 1 | 0 | 1 | 1 | 1 |
| 5008810 | F | N | Y | 0 | 270000 | Commercial associate | Secondary / secondary special | Single / not married | House / apartment | -19110 | -3051 | 1 | 0 | 1 | 1 | 1 |
Numeric transformation
Ahora vamos a convertir en años las variables DAYS_BIRTH y DAYS_EMPLOYED:
application_record <- application_record |>
mutate(YEARS_BIRTH = -DAYS_BIRTH/365,
YEARS_EMPLOYED = ifelse(DAYS_EMPLOYED > 0, 0, -DAYS_EMPLOYED/365))
application_record |>
head() |>
kable(format="markdown") |>
kable_styling("striped") |>
scroll_box(width = "100%")
| ID | CODE_GENDER | FLAG_OWN_CAR | FLAG_OWN_REALTY | CNT_CHILDREN | AMT_INCOME_TOTAL | NAME_INCOME_TYPE | NAME_EDUCATION_TYPE | NAME_FAMILY_STATUS | NAME_HOUSING_TYPE | DAYS_BIRTH | DAYS_EMPLOYED | FLAG_MOBIL | FLAG_WORK_PHONE | FLAG_PHONE | FLAG_EMAIL | CNT_FAM_MEMBERS | YEARS_BIRTH | YEARS_EMPLOYED |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 5008804 | M | Y | Y | 0 | 427500 | Working | Higher education | Civil marriage | Rented apartment | -12005 | -4542 | 1 | 1 | 0 | 0 | 2 | 32.89041 | 12.443836 |
| 5008805 | M | Y | Y | 0 | 427500 | Working | Higher education | Civil marriage | Rented apartment | -12005 | -4542 | 1 | 1 | 0 | 0 | 2 | 32.89041 | 12.443836 |
| 5008806 | M | Y | Y | 0 | 112500 | Working | Secondary / secondary special | Married | House / apartment | -21474 | -1134 | 1 | 0 | 0 | 0 | 2 | 58.83288 | 3.106849 |
| 5008808 | F | N | Y | 0 | 270000 | Commercial associate | Secondary / secondary special | Single / not married | House / apartment | -19110 | -3051 | 1 | 0 | 1 | 1 | 1 | 52.35616 | 8.358904 |
| 5008809 | F | N | Y | 0 | 270000 | Commercial associate | Secondary / secondary special | Single / not married | House / apartment | -19110 | -3051 | 1 | 0 | 1 | 1 | 1 | 52.35616 | 8.358904 |
| 5008810 | F | N | Y | 0 | 270000 | Commercial associate | Secondary / secondary special | Single / not married | House / apartment | -19110 | -3051 | 1 | 0 | 1 | 1 | 1 | 52.35616 | 8.358904 |
Una vez convertidas, eliminamos del conjunto de datos las variables iniciales:
application_record$DAYS_BIRTH <- NULL
application_record$DAYS_EMPLOYED <- NULL
Finalmente, vamos a particionar la variable ingreso:
application_record$INCOME_BIN <- cut(log(application_record$AMT_INCOME_TOTAL),breaks = 5)
Summarizing dataset
Veamos cómo quedaron nuestro predictores:
as.data.frame(summary(application_record)) |>
filter(!is.na(Freq)) |>
select(-ID, Var2, Freq) |>
kable(format="markdown") |>
kable_styling("striped") |>
scroll_box(width = "100%")
| Variable | Indicador |
|---|---|
| CODE_GENDER | F:294440 |
| CODE_GENDER | M:144117 |
| FLAG_OWN_CAR | N:275459 |
| FLAG_OWN_CAR | Y:163098 |
| FLAG_OWN_REALTY | N:134483 |
| FLAG_OWN_REALTY | Y:304074 |
| CNT_CHILDREN | Min. : 0.0000 |
| CNT_CHILDREN | 1st Qu.: 0.0000 |
| CNT_CHILDREN | Median : 0.0000 |
| CNT_CHILDREN | Mean : 0.4274 |
| CNT_CHILDREN | 3rd Qu.: 1.0000 |
| CNT_CHILDREN | Max. :19.0000 |
| AMT_INCOME_TOTAL | Min. : 26100 |
| AMT_INCOME_TOTAL | 1st Qu.: 121500 |
| AMT_INCOME_TOTAL | Median : 160780 |
| AMT_INCOME_TOTAL | Mean : 187524 |
| AMT_INCOME_TOTAL | 3rd Qu.: 225000 |
| AMT_INCOME_TOTAL | Max. :6750000 |
| NAME_INCOME_TYPE | Commercial associate:100757 |
| NAME_INCOME_TYPE | Pensioner : 75493 |
| NAME_INCOME_TYPE | State servant : 36186 |
| NAME_INCOME_TYPE | Student : 17 |
| NAME_INCOME_TYPE | Working :226104 |
| NAME_EDUCATION_TYPE | Academic degree : 312 |
| NAME_EDUCATION_TYPE | Higher education :117522 |
| NAME_EDUCATION_TYPE | Incomplete higher : 14851 |
| NAME_EDUCATION_TYPE | Lower secondary : 4051 |
| NAME_EDUCATION_TYPE | Secondary / secondary special:301821 |
| NAME_FAMILY_STATUS | Civil marriage : 36532 |
| NAME_FAMILY_STATUS | Married :299828 |
| NAME_FAMILY_STATUS | Separated : 27251 |
| NAME_FAMILY_STATUS | Single / not married: 55271 |
| NAME_FAMILY_STATUS | Widow : 19675 |
| NAME_HOUSING_TYPE | Co-op apartment : 1539 |
| NAME_HOUSING_TYPE | House / apartment :393831 |
| NAME_HOUSING_TYPE | Municipal apartment: 14214 |
| NAME_HOUSING_TYPE | Office apartment : 3922 |
| NAME_HOUSING_TYPE | Rented apartment : 5974 |
| NAME_HOUSING_TYPE | With parents : 19077 |
| FLAG_MOBIL | 1:438557 |
| FLAG_WORK_PHONE | 0:348156 |
| FLAG_WORK_PHONE | 1: 90401 |
| FLAG_PHONE | 0:312353 |
| FLAG_PHONE | 1:126204 |
| FLAG_EMAIL | 0:391102 |
| FLAG_EMAIL | 1: 47455 |
| CNT_FAM_MEMBERS | Min. : 1.000 |
| CNT_FAM_MEMBERS | 1st Qu.: 2.000 |
| CNT_FAM_MEMBERS | Median : 2.000 |
| CNT_FAM_MEMBERS | Mean : 2.194 |
| CNT_FAM_MEMBERS | 3rd Qu.: 3.000 |
| CNT_FAM_MEMBERS | Max. :20.000 |
| YEARS_BIRTH | Min. :20.52 |
| YEARS_BIRTH | 1st Qu.:34.28 |
| YEARS_BIRTH | Median :42.82 |
| YEARS_BIRTH | Mean :43.83 |
| YEARS_BIRTH | 3rd Qu.:53.38 |
| YEARS_BIRTH | Max. :69.04 |
| YEARS_EMPLOYED | Min. : 0.000 |
| YEARS_EMPLOYED | 1st Qu.: 1.016 |
| YEARS_EMPLOYED | Median : 4.019 |
| YEARS_EMPLOYED | Mean : 5.952 |
| YEARS_EMPLOYED | 3rd Qu.: 8.501 |
| YEARS_EMPLOYED | Max. :48.030 |
| INCOME_BIN | (10.2,11.3]: 22593 |
| INCOME_BIN | (11.3,12.4]:326179 |
| INCOME_BIN | (12.4,13.5]: 88552 |
| INCOME_BIN | (13.5,14.6]: 1193 |
| INCOME_BIN | (14.6,15.7]: 40 |
Joining the dataset
Realizando un inner_join para unir nuestro target con nuestros predictores:
data <- dplyr::inner_join(target_30dpd_12m,application_record, by="ID")
data |>
head() |>
kable(format="markdown") |>
kable_styling("striped") |>
scroll_box(width = "100%")
| ID | mora | CODE_GENDER | FLAG_OWN_CAR | FLAG_OWN_REALTY | CNT_CHILDREN | AMT_INCOME_TOTAL | NAME_INCOME_TYPE | NAME_EDUCATION_TYPE | NAME_FAMILY_STATUS | NAME_HOUSING_TYPE | FLAG_MOBIL | FLAG_WORK_PHONE | FLAG_PHONE | FLAG_EMAIL | CNT_FAM_MEMBERS | YEARS_BIRTH | YEARS_EMPLOYED | INCOME_BIN |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 5008804 | Yes | M | Y | Y | 0 | 427500 | Working | Higher education | Civil marriage | Rented apartment | 1 | 1 | 0 | 0 | 2 | 32.89041 | 12.443836 | (12.4,13.5] |
| 5008805 | Yes | M | Y | Y | 0 | 427500 | Working | Higher education | Civil marriage | Rented apartment | 1 | 1 | 0 | 0 | 2 | 32.89041 | 12.443836 | (12.4,13.5] |
| 5008806 | No | M | Y | Y | 0 | 112500 | Working | Secondary / secondary special | Married | House / apartment | 1 | 0 | 0 | 0 | 2 | 58.83288 | 3.106849 | (11.3,12.4] |
| 5008809 | No | F | N | Y | 0 | 270000 | Commercial associate | Secondary / secondary special | Single / not married | House / apartment | 1 | 0 | 1 | 1 | 1 | 52.35616 | 8.358904 | (12.4,13.5] |
| 5008810 | No | F | N | Y | 0 | 270000 | Commercial associate | Secondary / secondary special | Single / not married | House / apartment | 1 | 0 | 1 | 1 | 1 | 52.35616 | 8.358904 | (12.4,13.5] |
| 5008811 | No | F | N | Y | 0 | 270000 | Commercial associate | Secondary / secondary special | Single / not married | House / apartment | 1 | 0 | 1 | 1 | 1 | 52.35616 | 8.358904 | (12.4,13.5] |
Se debe remover también la variable ID, AMT_INCOME_TOTAL y FLAG_MOBIL puesto que no entrarán en el análisis:
data$ID <- NULL
data$AMT_INCOME_TOTAL <- NULL
data$FLAG_MOBIL <- NULL
Correlation analysis
Una vez que tenemos el conjunto de datos listo, veamos cómo se comportan nuestras variables tanto unilateralmente como en relación al target.
Y en relación al target:
num_var <- c("CNT_CHILDREN","YEARS_BIRTH","YEARS_EMPLOYED","CNT_FAM_MEMBERS")
data |>
select(num_var,mora) |>
pivot_longer(-mora, names_to = "variable", values_to = "value") %>%
ggplot(aes(x = mora, y = value)) +
geom_boxplot() +
facet_wrap(~ variable, scales = "free")
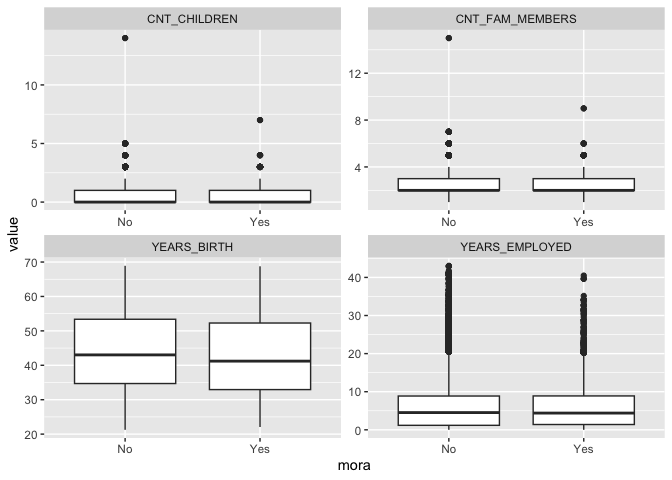
Viendo el análisis de correlación
data_num <- mutate_all(data,as.integer)
ggcorrplot::ggcorrplot(round(cor(data_num),2),
colors = c("red","white","steelblue"),
method ="circle",
outline.color = "black",
type = "upper",
ggtheme = ggplot2::theme_bw(),
lab = TRUE,
lab_size = 3,
pch = 100)
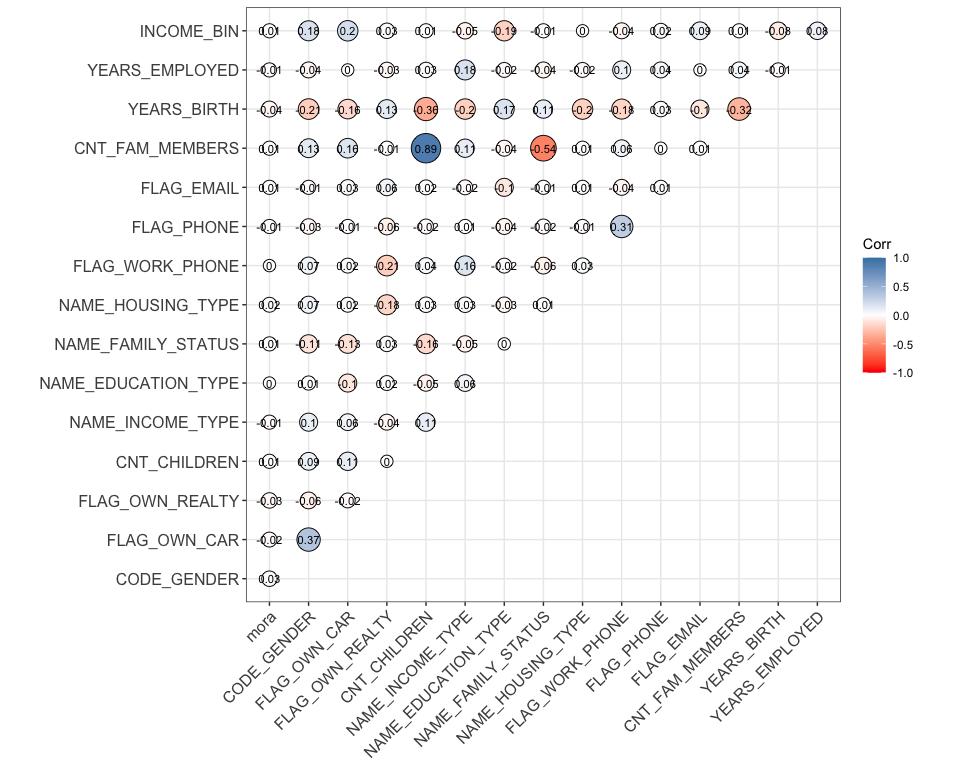
Modelación
Para realizar la modelación se utilizará la librería caret (que lleva su nombre por Classification And Regression Training). Una buena introducción puede encontrarse aquí.
El proceso de modelación se simplificará bastante, pues el objetivo es interpretar el modelo final. Básicamente, realizaremos una partición de los datos abordando el class-imbalance antes identificado utilizando el método de muestreo SMOTE.
Dividir los datos
Inicialmente se dividen los datos utilizando un $70\%$ de los mismos para entrenar el modelo y el resto para evaluarlo:
set.seed(1234)
trainIndex <- caret::createDataPartition(data$mora,
p = .7,
list = FALSE,
times = 1)
trainData <- data[trainIndex, ]
testData <- data[-trainIndex, ]
Validación cruzada
Ahora utilizamos la función trainControl donde especificamos algunas opciones que se utilizarán durante el entrenamiento. Particularmente utilizamos el método cv para realizará la validación cruzada utilizando el estándar k-Fold Cross-Validation con $k=10$ y el método de remuestreo SMOTE para abordar el class-imbalance:
cv <- caret::trainControl(method = "cv",
number = 10,
sampling = "smote")
Entrenamiento del modelo
Ahora, entrenamos un modelo logit utilizando la función train utilizando todos los predictores del conjunto de datos de entrenamiento:
logistic_model <- caret::train(mora ~ .,
data = trainData,
method = "glm",
family="binomial",
trControl = cv)
Evaluación
Una vez nuestro modelo entrenado, vamos a revisar qué contiene:
model_summ <- summary(logistic_model)
model_summ_df <- as.data.frame(model_summ$coefficients)
Variable <- rownames(model_summ_df)
rownames(model_summ_df) <- NULL
model_summ_df <- cbind(Variable,model_summ_df) |>
mutate_if(is.double, round,2)
model_summ_df |>
kable(format="markdown") |>
kable_styling("striped") |>
scroll_box(width = "100%")
| Variable | Estimate | Std. Error | z value | Pr(>|z|) |
|---|---|---|---|---|
| (Intercept) | -0.07 | 0.55 | -0.13 | 0.89 |
| CODE_GENDERM | 0.29 | 0.03 | 10.95 | 0.00 |
| FLAG_OWN_CARY | -0.33 | 0.03 | -12.42 | 0.00 |
| FLAG_OWN_REALTYY | -0.18 | 0.03 | -7.25 | 0.00 |
| CNT_CHILDREN | -0.35 | 0.14 | -2.48 | 0.01 |
| NAME_INCOME_TYPEPensioner | 0.02 | 0.05 | 0.38 | 0.70 |
NAME_INCOME_TYPEState servant | 0.04 | 0.05 | 0.86 | 0.39 |
| NAME_INCOME_TYPEStudent | -11.59 | 65.24 | -0.18 | 0.86 |
| NAME_INCOME_TYPEWorking | -0.07 | 0.03 | -2.43 | 0.01 |
NAME_EDUCATION_TYPEHigher education | -1.03 | 0.42 | -2.45 | 0.01 |
NAME_EDUCATION_TYPEIncomplete higher | -0.70 | 0.42 | -1.66 | 0.10 |
NAME_EDUCATION_TYPELower secondary | -1.37 | 0.44 | -3.13 | 0.00 |
NAME_EDUCATION_TYPESecondary / secondary special | -0.83 | 0.42 | -1.97 | 0.05 |
| NAME_FAMILY_STATUSMarried | -0.04 | 0.04 | -0.89 | 0.38 |
| NAME_FAMILY_STATUSSeparated | -0.03 | 0.15 | -0.18 | 0.86 |
NAME_FAMILY_STATUSSingle / not married | 0.29 | 0.14 | 1.99 | 0.05 |
| NAME_FAMILY_STATUSWidow | 0.39 | 0.16 | 2.49 | 0.01 |
NAME_HOUSING_TYPEHouse / apartment | 0.91 | 0.20 | 4.46 | 0.00 |
NAME_HOUSING_TYPEMunicipal apartment | 0.75 | 0.21 | 3.48 | 0.00 |
NAME_HOUSING_TYPEOffice apartment | 1.02 | 0.24 | 4.21 | 0.00 |
NAME_HOUSING_TYPERented apartment | 0.63 | 0.23 | 2.76 | 0.01 |
NAME_HOUSING_TYPEWith parents | 0.69 | 0.21 | 3.29 | 0.00 |
| FLAG_WORK_PHONE1 | -0.14 | 0.03 | -4.44 | 0.00 |
| FLAG_PHONE1 | -0.18 | 0.03 | -6.71 | 0.00 |
| FLAG_EMAIL1 | 0.05 | 0.04 | 1.26 | 0.21 |
| CNT_FAM_MEMBERS | 0.37 | 0.14 | 2.65 | 0.01 |
| YEARS_BIRTH | -0.01 | 0.00 | -7.29 | 0.00 |
| YEARS_EMPLOYED | 0.00 | 0.00 | -0.02 | 0.98 |
INCOME_BIN(11.3,12.4] | 0.10 | 0.05 | 1.81 | 0.07 |
INCOME_BIN(12.4,13.5] | -0.03 | 0.06 | -0.48 | 0.63 |
INCOME_BIN(13.5,14.6] | 1.62 | 0.22 | 7.31 | 0.00 |
Ahora, veamos la capacidad del modelo recién calibrado para realizar predicciones:
predictions <- predict(logistic_model, newdata=testData, type="prob")
predictions <- cbind(predictions,Moroso =testData$mora)
predictions |>
head() |>
kable(format="markdown") |>
kable_styling("striped") |>
scroll_box(width = "100%")
| No | Yes | Moroso |
|---|---|---|
| 0.6294876 | 0.3705124 | Yes |
| 0.5556730 | 0.4443270 | No |
| 0.5556730 | 0.4443270 | No |
| 0.6652800 | 0.3347200 | No |
| 0.4806780 | 0.5193220 | No |
| 0.4806780 | 0.5193220 | No |
Nótese que, para poder evaluar el modelo, se necesita realizar un punto de corte. Por ejemplo, en el caso más simple podemos elegir:
Si la probabilidad de que el individuo entre en mora es mayor a un $50\%$ se cataloga al individuo como moroso
En base a ese criterio, los resultados son:
preds <- ifelse(predictions$Yes > 0.5,"Yes","No")
draw_confusion_matrix(caret::confusionMatrix(data = factor(preds, levels = c("Yes","No")), reference =testData$mora, positive = "Yes"))
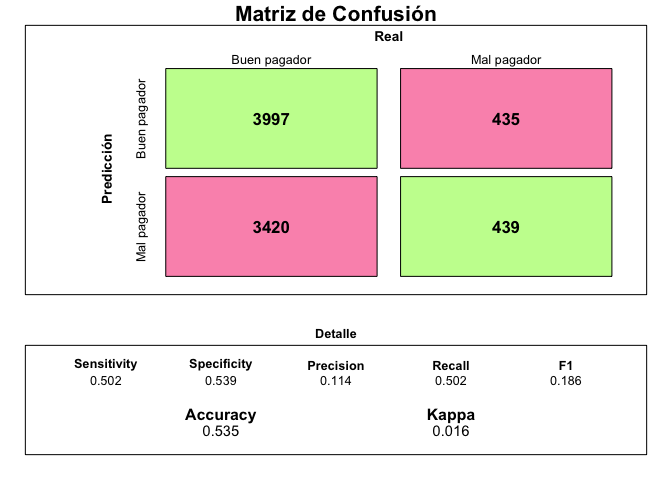
¿Cómo se interpreta? Aunque el detalle de las métricas se muestra en el gráfico anterior, la interpretación es intuitiva. El modelo identificó correctamente a $3997$ clientes como buenos pagadores y a $435$ clientes como pagadores en los datos de testeo. Sin embargo, indicó que $3420$ individuos iban a ser malos pagadores cuando en realidad fueron buenos mientras que que $439$ iban a ser buenos pagadores cuando en realidad fueron malos.
Otra forma de verlo es separar a los buenos pagadores de los malos diferenciando por la probabilidad que les asignó el modelo:
predictions |>
ggplot(aes(x= Yes, fill=Moroso))+
geom_histogram(color = "black", bins =50)+
scale_fill_manual(values=c("steelblue", "gray80"))+
labs(x= "\nProbabilidad de impago\n",
y = "Frecuencia\n")+
theme_bw()
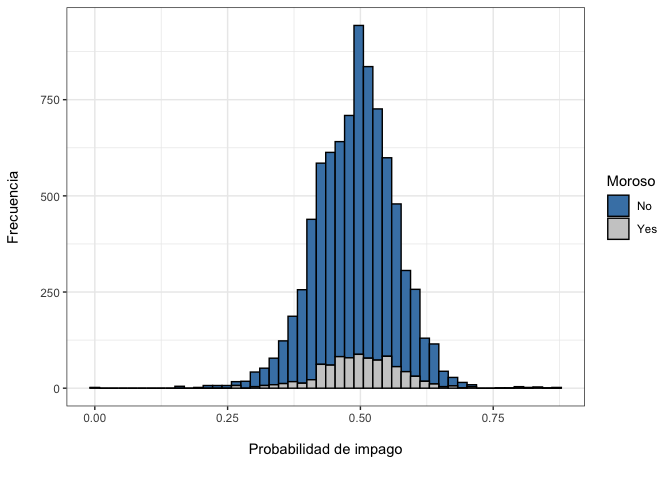
¿Cómo se interpreta? En el ideal, si el modelo fuera perfecto, ambos histogramas (el de los que sí son morosos y el de los que no son morosos) deberían estar separados, indicando que el modelo ha logrado identificar correctamente a cada grupo. En este caso ambas distribuciones están solapadas, lo que indica justamente lo contrario: el modelo no está distinguiendo a los buenos de los malos pagadores.
Construcción del Scorecard
Alternativamente al método logit, existe una metodología utilizada particularmente en la industria financiera que enfatiza el uso del Weight on Evidence (WoE) y del Information Value (IV) como indicadores de la influencia o peso que tiene cada predictor sobre nuestro target o variable de impago.4
Al final, el objetivo es construir scorecards con puntajes específicos que produzcan un determinado score para el usuario pero, en vez de tener una probabilidad, se tenga un puntaje. Visto de otra manera, el objetivo sería transformar los resultados del modelo logit a puntajes.
La explicación que sigue se basa en la discusión que se encuentra en Siddiqi (2017). Se debe decir que la construcción y cálculo del IV o WoE se debe realizar durante el proceso de feature engineering realizado previamente, por tanto, no es un sustituto sino un complemento al análisis ya realizado.
Creando nuevamente el dataset:
data_sc <- dplyr::inner_join(target_30dpd_12m,application_record, by="ID")
data_sc$ID <- NULL
data_sc$INCOME_BIN <- NULL
data_sc$FLAG_MOBIL <- NULL
data_sc |>
head() |>
kable(format="markdown") |>
kable_styling("striped") |>
scroll_box(width = "100%")
| mora | CODE_GENDER | FLAG_OWN_CAR | FLAG_OWN_REALTY | CNT_CHILDREN | AMT_INCOME_TOTAL | NAME_INCOME_TYPE | NAME_EDUCATION_TYPE | NAME_FAMILY_STATUS | NAME_HOUSING_TYPE | FLAG_WORK_PHONE | FLAG_PHONE | FLAG_EMAIL | CNT_FAM_MEMBERS | YEARS_BIRTH | YEARS_EMPLOYED |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Yes | M | Y | Y | 0 | 427500 | Working | Higher education | Civil marriage | Rented apartment | 1 | 0 | 0 | 2 | 32.89041 | 12.443836 |
| Yes | M | Y | Y | 0 | 427500 | Working | Higher education | Civil marriage | Rented apartment | 1 | 0 | 0 | 2 | 32.89041 | 12.443836 |
| No | M | Y | Y | 0 | 112500 | Working | Secondary / secondary special | Married | House / apartment | 0 | 0 | 0 | 2 | 58.83288 | 3.106849 |
| No | F | N | Y | 0 | 270000 | Commercial associate | Secondary / secondary special | Single / not married | House / apartment | 0 | 1 | 1 | 1 | 52.35616 | 8.358904 |
| No | F | N | Y | 0 | 270000 | Commercial associate | Secondary / secondary special | Single / not married | House / apartment | 0 | 1 | 1 | 1 | 52.35616 | 8.358904 |
| No | F | N | Y | 0 | 270000 | Commercial associate | Secondary / secondary special | Single / not married | House / apartment | 0 | 1 | 1 | 1 | 52.35616 | 8.358904 |
Weight on Evidence (WoE)
El primer paso para calcular ambos indicadores es agrupar las variables en “bins” o grupos que tengan algún sentido para el modelador. Se recomienda iniciar con 20 grupos y luego ir modificando en función a las métricas obtenidas. La función scorecard::woebin() realiza esta partición:
bins <- scorecard::woebin(data_sc,"mora",positive = "Yes|1")
## ✔ Binning on 27638 rows and 16 columns in 00:00:11
Por ejemplo, veamos los grupos que se formaron del ingreso de los individuos:
bins$AMT_INCOME_TOTAL |>
mutate_if(is.double, round, 4) |>
select(-variable,-breaks,-is_special_values,-total_iv,-bin_iv) |>
janitor::adorn_totals() |>
kable(format="markdown") |>
kable_styling("striped") |>
scroll_box(width = "100%")
| bin | count | count_distr | neg | pos | posprob | woe |
|---|---|---|---|---|---|---|
| [-Inf,90000) | 1994 | 0.0721 | 1777 | 217 | 0.1088 | 0.0355 |
| [90000,120000) | 4582 | 0.1658 | 4133 | 449 | 0.0980 | -0.0815 |
| [120000,140000) | 4267 | 0.1544 | 3794 | 473 | 0.1109 | 0.0562 |
| [140000,200000) | 6362 | 0.2302 | 5759 | 603 | 0.0948 | -0.1184 |
| [200000,250000) | 5260 | 0.1903 | 4629 | 631 | 0.1200 | 0.1455 |
| [250000, Inf) | 5173 | 0.1872 | 4632 | 541 | 0.1046 | -0.0091 |
| Total | 27638 | 1.0000 | 24724 | 2914 | 0.6371 | 0.0282 |
En la tabla anterior hay bastante información. Nótese que la la columna pos se refiere al número de individuos que han estado en mora en los primeros 12 meses de haber obtenido la tarjeta en cada uno de los grupos. La columna posprob es la proporción de estos individuos considerando el total a los individuos de ese grupo, es decir count. El WoE se calcula como:
$$WoE = \ln\Big(\frac{\textit{Clase Positiva}}{\textit{Clase Negativa}}\Big)\times 100 $$
Se debe tomar en cuenta que la clase positiva es la clase que se desea predecir, en este caso el impago.
Por ejemplo, en el caso del grupo que va entre $[90.000,120.000)$:
$$\begin{aligned} WoE &= \ln\Big( \frac{\frac{217}{2914}}{\frac{1777}{24724}}\Big) \times 100 \\ &= \ln\Big(\frac{0.074}{0.072} \Big) \times 100 \\ß &= 0.35 \end{aligned}$$
Cuando el resultado es positivo indica que, para ese grupo, la proporción de individuos en la clase positiva es mayor que la proporción de los individuos en la clase negativa. Así, en este rango, hay más individuos morosos que los que no lo son.
Viendo el resumen gráfico:
bins$AMT_INCOME_TOTAL |>
ggplot(aes(x= bin, y = woe))+
geom_bar(stat= "identity", color = "black", fill="steelblue")+
theme_bw()
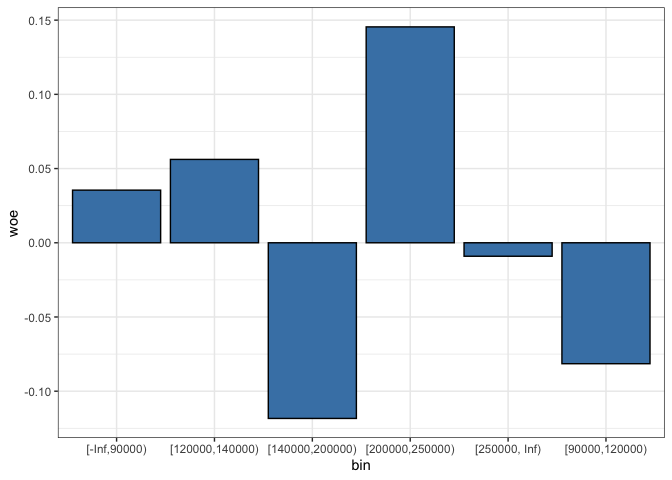
Nótese que en el gráfico anterior vemos que para los dos grupos de ingresos más bajos el WoE es positivo, lo que indica que la proporción de impagos en ese grupo es mayor a la proporción de individuos que pagan.
Lo que esperaríamos ver, sin embargo, es una tendencia negativa entre los grupos de ingreso más alto y el WoE, lo que indicaría que, a medida que el ingreso se incrementa, la proporción de individuos que son buenos pagadores se hace más grande en relación a la proporción de malos pagadores. Sin embargo, eso no ocurre en nuestro caso.3
Este análisis se debe realizar para todas las variables:
bins_df <- bind_rows(bins)
bins_df |>
select(variable, bin,woe) |>
ggplot(aes(x = bin, y=woe)) +
geom_bar(stat= "identity", color= "black", fill="steelblue") +
facet_wrap(~ variable, scales = "free_x")+
theme_bw()+
theme(axis.text.x = element_text(angle = 45))
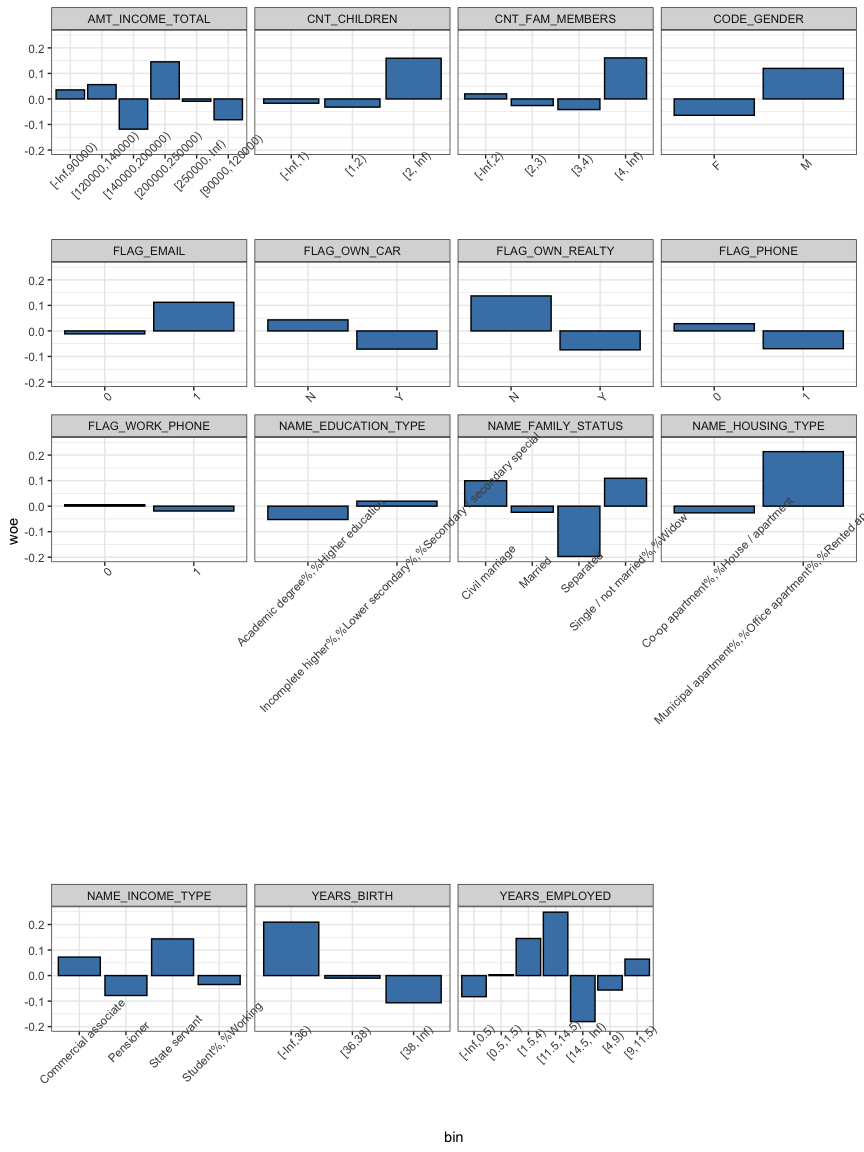
Con esta información se debe buscar “arreglar” las variables que no tengan tanto sentido con diferentes grupos.
Information Value (IV)
El indicador IV muestra la fuerza total de la característica en función al target o variable de impago. Su uso proviene de la teoría de la información y se calcula como:
$$IV = \sum_{i=1}^{n} (\textit{Dist. Good}_{i} - \textit{Dist. Bad}_{i}) \times \ln\Big(\frac{\textit{Dist. Good}_{i}}{\textit{Dist. Bad}_{i}}\Big)$$
El criterio que se suele utilizar para ver la predictibilidad de cada variable es:
| Rango | Predictibilidad |
|---|---|
| < 0.02 | No predictivo |
| 0.02-0.1 | Baja |
| 0.1 - 0.3 | Media |
| > 0.3 | Alta |
Sin embargo, cuando la característica tiene un $IV > 0.5$ se debe revisar cuidadosamente.
En el caso de nuestros datos el IV es:
infv <- scorecard::iv(data_sc, y = "mora", positive = "Yes|1") |>
as_tibble()
infv |>
mutate_if(is.double, round, 3) |>
arrange(desc(info_value)) |>
kable(format="markdown") |>
kable_styling("striped")
| Variable | IV |
|---|---|
| YEARS_EMPLOYED | 0.875 |
| YEARS_BIRTH | 0.869 |
| AMT_INCOME_TOTAL | 0.150 |
| FLAG_OWN_REALTY | 0.010 |
| CODE_GENDER | 0.008 |
| NAME_FAMILY_STATUS | 0.007 |
| NAME_EDUCATION_TYPE | 0.007 |
| NAME_HOUSING_TYPE | 0.006 |
| CNT_FAM_MEMBERS | 0.006 |
| CNT_CHILDREN | 0.006 |
| NAME_INCOME_TYPE | 0.005 |
| FLAG_OWN_CAR | 0.003 |
| FLAG_PHONE | 0.002 |
| FLAG_EMAIL | 0.001 |
| FLAG_WORK_PHONE | 0.000 |
Con esto datos vemos que las variables, en general, presentan poco poder predictivo.
Modelación
Inicialmente, debemos construir un conjunto de datos pero utilizando el valor del $WoE$ en vez del valor numérico de la variable:
data_woe <- woebin_ply(data_sc, bins ) %>%
as_tibble()
## ✔ Woe transformating on 27638 rows and 15 columns in 00:00:10
Los datos quedan como:
data_woe |>
head() |>
kable(format="markdown") |>
kable_styling("striped") |>
scroll_box(width = "100%")
| mora | CODE_GENDER_woe | FLAG_OWN_CAR_woe | FLAG_OWN_REALTY_woe | CNT_CHILDREN_woe | AMT_INCOME_TOTAL_woe | NAME_INCOME_TYPE_woe | NAME_EDUCATION_TYPE_woe | NAME_FAMILY_STATUS_woe | NAME_HOUSING_TYPE_woe | FLAG_WORK_PHONE_woe | FLAG_PHONE_woe | FLAG_EMAIL_woe | CNT_FAM_MEMBERS_woe | YEARS_BIRTH_woe | YEARS_EMPLOYED_woe |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Yes | 0.1196992 | -0.0712469 | -0.0741842 | -0.0167474 | -0.0090770 | -0.0350806 | -0.0524537 | 0.0994392 | 0.2135455 | -0.0190648 | 0.0284101 | -0.0116079 | -0.0258573 | 0.2092954 | 0.2483318 |
| Yes | 0.1196992 | -0.0712469 | -0.0741842 | -0.0167474 | -0.0090770 | -0.0350806 | -0.0524537 | 0.0994392 | 0.2135455 | -0.0190648 | 0.0284101 | -0.0116079 | -0.0258573 | 0.2092954 | 0.2483318 |
| No | 0.1196992 | -0.0712469 | -0.0741842 | -0.0167474 | -0.0814882 | -0.0350806 | 0.0194958 | -0.0240393 | -0.0262420 | 0.0056076 | 0.0284101 | -0.0116079 | -0.0258573 | -0.1065324 | 0.1450917 |
| No | -0.0640447 | 0.0432688 | -0.0741842 | -0.0167474 | -0.0090770 | 0.0724259 | 0.0194958 | 0.1090728 | -0.0262420 | 0.0056076 | -0.0695418 | 0.1121048 | 0.0198040 | -0.1065324 | -0.0566819 |
| No | -0.0640447 | 0.0432688 | -0.0741842 | -0.0167474 | -0.0090770 | 0.0724259 | 0.0194958 | 0.1090728 | -0.0262420 | 0.0056076 | -0.0695418 | 0.1121048 | 0.0198040 | -0.1065324 | -0.0566819 |
| No | -0.0640447 | 0.0432688 | -0.0741842 | -0.0167474 | -0.0090770 | 0.0724259 | 0.0194958 | 0.1090728 | -0.0262420 | 0.0056076 | -0.0695418 | 0.1121048 | 0.0198040 | -0.1065324 | -0.0566819 |
Ahora, vamos a iniciar el proceso de modelaje nuevamente.
# Dividir los datos en train y test dataset
set.seed(1234)
trainIndex_woe <- createDataPartition(data_woe$mora,
p = .7,
list = FALSE,
times = 1)
trainData_woe <- data_woe[trainIndex_woe, ]
testData_woe <- data_woe[-trainIndex_woe, ]
# Crear un objeto para realizar 10-fold cv
cv_woe <- trainControl(method = "cv", number = 10, sampling = "smote")
# Entrenar el modelo con los datos woe
logistic_model_woe <- train(mora ~ .,
data = trainData_woe,
method = "glm",
family="binomial",
trControl = cv_woe)
#Realizar las predicciones con un punto de corte de 0.5%
predictions_woe <- predict(logistic_model_woe, newdata=testData_woe, type="prob")
preds_woe <- ifelse(predictions_woe$Yes > 0.5,"Yes","No")
# Evaluar el modelo
draw_confusion_matrix(caret::confusionMatrix(data = factor(preds_woe, levels = c("Yes","No")), reference =testData_woe$mora, positive = "Yes"))
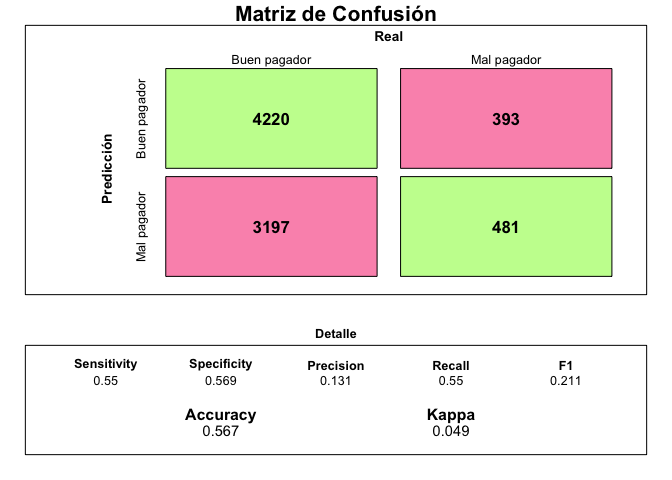
Que es ligeramente mejor que el modelo entrenando datos sin agrupar. El modelo es
model_summ_woe <- summary(logistic_model_woe)
model_summ_df_woe <- as.data.frame(model_summ_woe$coefficients)
Variable <- rownames(model_summ_df_woe)
rownames(model_summ_df_woe) <- NULL
model_summ_df_woe <- cbind(Variable,model_summ_df_woe) |>
mutate_if(is.double, round,2)
model_summ_df_woe |>
kable(format="markdown") |>
kable_styling("striped") |>
scroll_box(width = "100%")
| Variable | Estimate | Std. Error | z value | Pr(>|z|) |
|---|---|---|---|---|
| (Intercept) | 0.00 | 0.01 | -0.39 | 0.70 |
| CODE_GENDER_woe | 1.47 | 0.14 | 10.63 | 0.00 |
| FLAG_OWN_CAR_woe | 2.79 | 0.22 | 12.57 | 0.00 |
| FLAG_OWN_REALTY_woe | 0.89 | 0.11 | 7.78 | 0.00 |
| CNT_CHILDREN_woe | 1.49 | 0.55 | 2.70 | 0.01 |
| AMT_INCOME_TOTAL_woe | 1.03 | 0.12 | 8.82 | 0.00 |
| NAME_INCOME_TYPE_woe | 0.27 | 0.17 | 1.57 | 0.12 |
| NAME_EDUCATION_TYPE_woe | 3.43 | 0.37 | 9.21 | 0.00 |
| NAME_FAMILY_STATUS_woe | 0.96 | 0.16 | 6.05 | 0.00 |
| NAME_HOUSING_TYPE_woe | 0.27 | 0.15 | 1.74 | 0.08 |
| FLAG_WORK_PHONE_woe | 5.31 | 1.22 | 4.36 | 0.00 |
| FLAG_PHONE_woe | 1.20 | 0.27 | 4.45 | 0.00 |
| FLAG_EMAIL_woe | -0.05 | 0.33 | -0.17 | 0.87 |
| CNT_FAM_MEMBERS_woe | -0.44 | 0.53 | -0.84 | 0.40 |
| YEARS_BIRTH_woe | 0.67 | 0.08 | 8.25 | 0.00 |
| YEARS_EMPLOYED_woe | 0.75 | 0.10 | 7.64 | 0.00 |
Scorecard
El siguiente paso es construir el scorecard para el modelo. Para esto vamos a utilizar la librería scorecard. Sin embargo, vamos a volverlo a estimar con la librería glm por un tema de compatibilidad entre librerías:
set.seed(1234)
trainData_smote <- themis::smote(trainData_woe, "mora")
logistic_model_woe_glm <- glm( mora ~ CODE_GENDER_woe + FLAG_OWN_CAR_woe + FLAG_OWN_REALTY_woe +
CNT_CHILDREN_woe + AMT_INCOME_TOTAL_woe + NAME_INCOME_TYPE_woe +
NAME_EDUCATION_TYPE_woe + NAME_FAMILY_STATUS_woe + NAME_HOUSING_TYPE_woe +
FLAG_WORK_PHONE_woe + FLAG_PHONE_woe + FLAG_EMAIL_woe + CNT_FAM_MEMBERS_woe +
YEARS_BIRTH_woe + YEARS_EMPLOYED_woe, data = trainData_smote, family = 'binomial')
Ahora, realizamos la predicción
resp_glm <- predict(logistic_model_woe_glm, type = 'response')
predictions_woe_glm <- predict(logistic_model_woe_glm, newdata=testData_woe, type="response")
preds_woe_glm <- ifelse(predictions_woe_glm> 0.5,"Yes","No")
# Evaluar el modelo
draw_confusion_matrix(caret::confusionMatrix(data = factor(preds_woe_glm, levels = c("Yes","No")), reference =testData_woe$mora, positive = "Yes"))
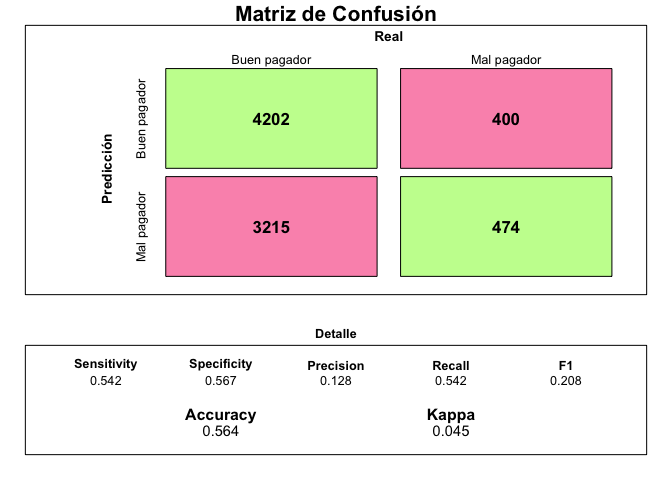
Que si bien no es igual al anterior por un tema de random sampling es bastante similar y ligeramente superior al modelo inicial.
Ahora vamos a reescalar el modelo para obtener el scorecard apuntando a un rango entre $300$ puntos y $850$ siendo $575$ puntos el punto donde hay $50\%$ de probabilidad de impago, según el modelo.
#1:1 significa 575
points0 = 850
odds0 = 1000
pdo = 27.59
card <- scorecard::scorecard( bins ,logistic_model_woe_glm,
points0 = points0,
odds0 =1/odds0, # el scorecard requiere la inversa
pdo = pdo)
sc <- scorecard::scorecard_ply(data_sc, card)
predictions_sc <- data.frame(score= sc$score,Moroso =data_sc$mora)
predictions_sc |>
ggplot(aes(x= score, fill=Moroso))+
geom_histogram(color = "black", bins =50)+
scale_fill_manual(values=c("steelblue", "gray80"))+
labs(x= "\nScore",
y = "Frecuencia\n")+
theme_bw()
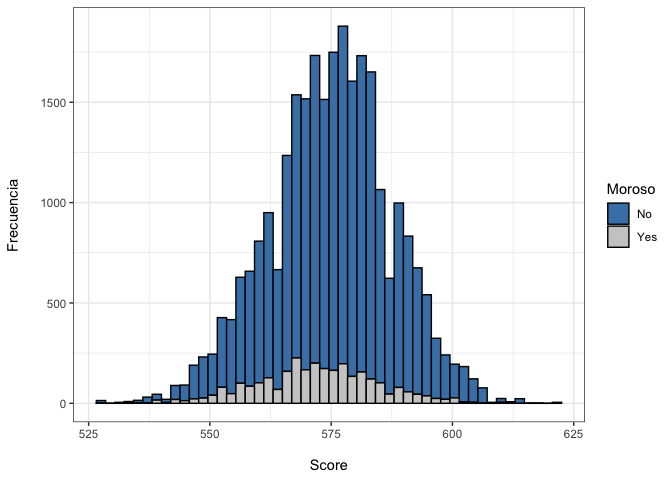
Como se observa, el modelo todavía no tiene tanta capacidad predictiva pero permite asignar un puntaje a cada individuo del conjunto de datos.
¿Cómo quedaría el scorecard?
score_card <- bind_rows(card) |>
select(variable, bin, points)
score_card |>
kable(format="markdown") |>
kable_styling("striped") |>
scroll_box(width = "100%")
| Variable | bin | points |
|---|---|---|
| basepoints | NA | 575 |
| CODE_GENDER | F | 4 |
| CODE_GENDER | M | -7 |
| FLAG_OWN_CAR | N | -5 |
| FLAG_OWN_CAR | Y | 7 |
| FLAG_OWN_REALTY | N | -5 |
| FLAG_OWN_REALTY | Y | 3 |
| CNT_CHILDREN | [-Inf,1) | 1 |
| CNT_CHILDREN | [1,2) | 2 |
| CNT_CHILDREN | [2, Inf) | -10 |
| AMT_INCOME_TOTAL | [-Inf,90000) | -1 |
| AMT_INCOME_TOTAL | [90000,120000) | 3 |
| AMT_INCOME_TOTAL | [120000,140000) | -2 |
| AMT_INCOME_TOTAL | [140000,200000) | 5 |
| AMT_INCOME_TOTAL | [200000,250000) | -6 |
| AMT_INCOME_TOTAL | [250000, Inf) | 0 |
| NAME_INCOME_TYPE | Commercial associate | -1 |
| NAME_INCOME_TYPE | Pensioner | 1 |
| NAME_INCOME_TYPE | State servant | -2 |
| NAME_INCOME_TYPE | Student%,%Working | 0 |
| NAME_EDUCATION_TYPE | Academic degree%,%Higher education | 7 |
| NAME_EDUCATION_TYPE | Incomplete higher%,%Lower secondary%,%Secondary / secondary special | -3 |
| NAME_FAMILY_STATUS | Civil marriage | -4 |
| NAME_FAMILY_STATUS | Married | 1 |
| NAME_FAMILY_STATUS | Separated | 7 |
| NAME_FAMILY_STATUS | Single / not married%,%Widow | -4 |
| NAME_HOUSING_TYPE | Co-op apartment%,%House / apartment | 0 |
| NAME_HOUSING_TYPE | Municipal apartment%,%Office apartment%,%Rented apartment%,%With parents | -2 |
| FLAG_WORK_PHONE | 0 | -1 |
| FLAG_WORK_PHONE | 1 | 4 |
| FLAG_PHONE | 0 | -2 |
| FLAG_PHONE | 1 | 4 |
| FLAG_EMAIL | 0 | 0 |
| FLAG_EMAIL | 1 | 0 |
| CNT_FAM_MEMBERS | [-Inf,2) | 0 |
| CNT_FAM_MEMBERS | [2,3) | -1 |
| CNT_FAM_MEMBERS | [3,4) | -1 |
| CNT_FAM_MEMBERS | [4, Inf) | 3 |
| YEARS_BIRTH | [-Inf,36) | -6 |
| YEARS_BIRTH | [36,38) | 0 |
| YEARS_BIRTH | [38, Inf) | 3 |
| YEARS_EMPLOYED | [-Inf,0.5) | 2 |
| YEARS_EMPLOYED | [0.5,1.5) | 0 |
| YEARS_EMPLOYED | [1.5,4) | -4 |
| YEARS_EMPLOYED | [4,9) | 2 |
| YEARS_EMPLOYED | [9,11.5) | -2 |
| YEARS_EMPLOYED | [11.5,14.5) | -7 |
| YEARS_EMPLOYED | [14.5, Inf) | 5 |
Por ejemplo, un individuo comienza con $575$ puntos, si es de sexo femenino ($CODE_GENDER = F$) suma $4$ puntos, si tiene un auto propio ($FLAG_OWN_CAR = Y$) gana otros $7$ puntos y así sucesivamente.
Si al final el nuevo solicitante acaba con más de $575$ puntos se le otorga la tarjeta de crédito.
Comentarios finales
Con este ejercicio se ha tratado de ilustrar de forma resumida el proceso de construcción de un scorecard para medir el riesgo de crédito. Aún cuando hay bastante espacio de mejora (análisis de outliers, mejor procesos de binning, reescalamiento y centrado de datos, probar con distintos modelos, etc.), se ha tratado de mantener el proceso lo más simple posible para ilustrar los distintos puntos:
- La definición de impago en la construcción del target es fundamental para el análisis
- La construcción de un scorecard es un proceso lento que requiere conocimiento experto y bastante información. La relación entre los datos no es necesariamente lineal por lo que la etapa de preprocesamiento es fundamental.
Regularmente las operaciones castigadas se quitan del balance, pues se asumen como pérdida con lo cual, para la gestión de la cartera se omite del análisis. En este caso, como lo que se desea detectar es el no repago, se lo mantiene.] ↩︎
Una mejor decisión implica crear una nueva categoría en los datos faltantes y luego verificar cuánto incide esa variable en la predicción. En el contexto crediticio, los datos faltantes pueden tener una explicación, por ejemplo, en la imputación se omite esa información porque es considerada “mala” por el ejecutivo comercial para solicitud de crédito, entre otras. ↩︎
En realidad, se deberían indagar sobre el porqué ocurre esto. Por ejemplo, puede ser que el proceso de agrupamiento se deba rehacer o haya que ajustar los WoE. Más sobre esto en Siddiqi (2016). ↩︎