Optimización de portafolios bajo el enfoque de Markowitz en R

Dos activos: implementación manual

Introducción

El objetivo de este taller es construir un portafolio de inversión optimizado que incluya distintos activos financieros. La exposición se base principalmente en el libro de Clifford Ang, pero va un poco más a detalle en este tema. Al lector interesado en profundizar en el tema y similares, se le recomienda leer el libro.

Librerías

En particular, se utilizará la librería quantmod para extraer información de Yahoo Finance, la cual provee una interfaz para este fin. Adicionalmente se utilizará la librería tidyverse que nos proporciona funciones como dplyr::mutate o ggplot2::ggplot para manipular y graficar los datos¹.

library(quantmod)

## Loading required package: xts

## Loading required package: zoo

## 
## Attaching package: 'zoo'

## The following objects are masked from 'package:base':
## 
##     as.Date, as.Date.numeric

## Loading required package: TTR

## Registered S3 method overwritten by 'quantmod':
##   method            from
##   as.zoo.data.frame zoo

Ahora cargamos la librería tidyverse:

library(tidyverse)

## ── Attaching core tidyverse packages ──────────────────────── tidyverse 2.0.0 ──
## ✔ dplyr     1.1.4     ✔ readr     2.1.5
## ✔ forcats   1.0.0     ✔ stringr   1.5.1
## ✔ ggplot2   3.5.1     ✔ tibble    3.2.1
## ✔ lubridate 1.9.3     ✔ tidyr     1.3.1
## ✔ purrr     1.0.2

## ── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
## ✖ dplyr::filter() masks stats::filter()
## ✖ dplyr::first()  masks xts::first()
## ✖ dplyr::lag()    masks stats::lag()
## ✖ dplyr::last()   masks xts::last()
## ℹ Use the conflicted package (<http://conflicted.r-lib.org/>) to force all conflicts to become errors

Finalmente, de manera predeterminada, $\textsf{R}$ muestra los números en notación científica. Para evitar esto, se debe cambiar la opción scipen:

options(scipen = 999)

Esta opción permite que los números se muestren en notación decimal. Para volver a la notación científica, se puede cambiar el valor de la opción a 0.

Preparación de los datos

Para obtener los datos de Yahoo Finance, se utiliza la función getSymbols de la librería quantmod.

Lo único que se necesita es el ticker de la acción que se desea analizar². Por ejemplo, en este caso se utilizarán tanto el SPDR S&P 500 ETF Trust (SPY) como el iShares +10 Year Investment Grade Corporate Bond ETF (IGLB).

SPY <- quantmod::getSymbols("SPY", 
                                src = "yahoo", 
                                auto.assign = FALSE)

IGLB <- quantmod::getSymbols("IGLB",
                                src = "yahoo",
                                auto.assign = FALSE)

Ahora mostramos los primeros y últimos datos de los activos. Primeramente, SPY:

head(SPY)

##            SPY.Open SPY.High SPY.Low SPY.Close SPY.Volume SPY.Adjusted
## 2007-01-03   142.25   142.86  140.57    141.37   94807600    100.56211
## 2007-01-04   141.23   142.05  140.61    141.67   69620600    100.77550
## 2007-01-05   141.33   141.40  140.38    140.54   76645300     99.97169
## 2007-01-08   140.82   141.41  140.25    141.19   71655000    100.43407
## 2007-01-09   141.31   141.60  140.40    141.07   75680100    100.34872
## 2007-01-10   140.58   141.57  140.30    141.54   72428000    100.68302

tail(SPY)

##            SPY.Open SPY.High SPY.Low SPY.Close SPY.Volume SPY.Adjusted
## 2025-02-03   592.67   600.29  590.49    597.77   65857200       597.77
## 2025-02-04   597.83   602.30  597.28    601.78   33457800       601.78
## 2025-02-05   600.64   604.37  598.58    604.22   30653100       604.22
## 2025-02-06   605.99   606.45  602.63    606.32   35771500       606.32
## 2025-02-07   606.89   608.13  600.05    600.77   50788500       600.77
## 2025-02-10   604.03   605.50  602.74    604.85   25960900       604.85

También, IGLB:

head(IGLB)

##            IGLB.Open IGLB.High IGLB.Low IGLB.Close IGLB.Volume IGLB.Adjusted
## 2009-12-09     51.03     51.03    50.90      50.90       10200      26.64499
## 2009-12-10     50.90     50.90    50.90      50.90           0      26.64499
## 2009-12-11     50.27     50.56    50.27      50.56        4400      26.46698
## 2009-12-14     50.85     50.87    50.85      50.87         500      26.62927
## 2009-12-15     50.87     50.87    50.87      50.87           0      26.62927
## 2009-12-16     51.14     51.14    50.95      50.95         400      26.67116

tail(IGLB)

##            IGLB.Open IGLB.High IGLB.Low IGLB.Close IGLB.Volume IGLB.Adjusted
## 2025-02-03     49.63     49.93    49.47      49.62      948600         49.62
## 2025-02-04     49.40     49.83    49.38      49.78     1008600         49.78
## 2025-02-05     50.16     50.46    50.15      50.31      409200         50.31
## 2025-02-06     50.32     50.42    50.13      50.23     1184800         50.23
## 2025-02-07     50.03     50.04    49.82      49.94      990400         49.94
## 2025-02-10     49.99     50.11    49.82      49.90      720600         49.90

Los datos de SPY inicial el 2007 y los de IGLB inician a finales de 2009. Para evitar no lidiar con problemas de datos faltantes, nos vamos a quedar con los últimos 5 años de información, esto es, desde el 2020:

SPY <- SPY["2014-12-31/2019"]
IGLB <- IGLB["2014-12-31/2019"]

Nótese que la forma en que se ha hecho la selección de datos no es estándar en $\textsf{R}$ y son más bien las propiedades heredadas de la clase xts. En este caso, se seleccionan los datos desde el 31 de diciembre de 2014 hasta el 31 de diciembre de 2019.

El análisis en esta sección se realizará con datos mensuales. Sin embargo, los datos de Yahoo Finance son diarios. Existen varias maneras de convertir estos datos en mensuales. Por ejemplo, una de ellas sería calcular el retorno diario y luego convertir estos datos en mensuales. Otra forma sería quedarnos con los datos de cierre de mes. En este caso, se utilizará la primera opción.

Para la implementación, sin embargo, se utilizará la función xts::to.monthly(), que hace el trabajo por nosotros:

SPY_m <- xts::to.monthly(SPY)
IGLB_m <- xts::to.monthly(IGLB)

tail(SPY_m)

##          SPY.Open SPY.High SPY.Low SPY.Close SPY.Volume SPY.Adjusted
## Jul 2019   296.68   302.23  294.33    297.43 1110102300     273.1441
## Aug 2019   297.60   300.87  281.72    292.45 2034004800     268.5707
## Sep 2019   290.57   302.63  289.27    296.77 1303830000     273.7966
## Oct 2019   297.74   304.55  284.82    303.33 1386748300     279.8487
## Nov 2019   304.92   315.48  304.74    314.31 1037123500     289.9788
## Dec 2019   314.59   323.80  307.13    321.86 1285175800     298.4043

tail(IGLB_m)

##          IGLB.Open IGLB.High IGLB.Low IGLB.Close IGLB.Volume IGLB.Adjusted
## Jul 2019     63.81     64.38    62.69      64.04     4463100      51.03732
## Aug 2019     64.11     68.33    64.08      67.65     7446600      54.09341
## Sep 2019     67.42     67.74    64.34      66.63     5428300      53.44373
## Oct 2019     65.99     67.12    65.44      66.56     7646400      53.54588
## Nov 2019     66.44     67.13    64.87      66.81     3629400      53.91549
## Dec 2019     66.05     67.36    65.81      66.67     8943200      54.10448

Ahora, realmente lo que necesitamos no son los precios, sino los rendimientos mensuales. Para ello, utilizamos la función quantmod::Delt(), aunque bien podríamos haber calculado los mismos de forma manual:

$$ r_t = \frac{P_t - P_{t-1}}{P_{t-1}} $$

Donde $r_t$ es el rendimiento en el tiempo $t$ y $P_t$ es el precio en el tiempo $t$.

Entonces, en el siguiente código se calculan los rendimientos de los activos y se almacenan en un data.frame llamado rets:

rets <- cbind(quantmod::Delt(SPY_m$SPY.Adjusted), 
              quantmod::Delt(IGLB_m$IGLB.Adjusted))

head(rets,2)

##          Delt.1.arithmetic Delt.1.arithmetic.1
## Dec 2014                NA                  NA
## Jan 2015       -0.02962922          0.05315335

tail(rets,2)

##          Delt.1.arithmetic Delt.1.arithmetic.1
## Nov 2019        0.03619847         0.006902604
## Dec 2019        0.02905549         0.003505400

La primera fila, correspondiente a los datos de diciembre de 2014 tienen un NA porque no se puede calcular el retorno del primer mes. Para evitar que este valor afecte el análisis, se elimina la primera fila de los retornos.

Adicionalmente, se renombran las columnas de los retornos:

rets <- rets[-1, ]
names(rets) <- c("SPY", "IGLB")

tail(rets)

##                  SPY         IGLB
## Jul 2019  0.01511941  0.007916730
## Aug 2019 -0.01674341  0.059879538
## Sep 2019  0.01945804 -0.012010496
## Oct 2019  0.02210457  0.001911498
## Nov 2019  0.03619847  0.006902604
## Dec 2019  0.02905549  0.003505400

Con esto ya tenemos listo nuestro conjunto de dos activos para realizar el análisis.

Construcción manual del Portafolio

En esta sección vamos a construir el portafolio de inversión manualmente. Aunque en la práctica existen herramientas que permiten hacerlo de forma automática, es importante entender cómo se construye paso a paso para ganar intuición.

Dado que se tiene información histórica del rendimiento de los activos y asumiendo que su riesgo puede ser capturado por la varianza histórica, se construirán $n$ portafolios asumiendo distintos “pesos” para cada activo. Luego se analizarán los portafolios y trataremos de encontrar el que maximice el retorno ajustado por riesgo, que es lo mismo que decir el que maximice el retorno dado un nivel de riesgo o el que minimice el riesgo dado un nivel de retorno.

Algo de teoría

Antes que nada, es importante entender qué se necesita teóricamente para construir un portafolio. En este caso, nos interesa calcular el retorno esperado y la varianza de un portafolio.

¿Cómo se obtiene el retorno esperado de un portafolio? Supongamos que se tienen dos activos, $A$ y $B$, con retornos esperados $E(R_A)$ y $E(R_B)$, respectivamente. Si se invierte una fracción $w_A$ en el activo $A$ y una fracción $w_B$ en el activo $B$, entonces el retorno esperado del portafolio es:

$$ E(R_p) = w_A \cdot E(R_A) + w_B \cdot E(R_B) $$

Ahora, ¿cómo se obtiene la varianza de un portafolio? Supongamos que la varianza de los activos $A$ y $B$ son $\sigma^2_A$ y $\sigma^2_B$, respectivamente. Entonces, la varianza de un portafolio es:

$$ \sigma^2_p = w_A^2 \cdot \sigma^2_A + w_B^2 \cdot \sigma^2_B + 2 \cdot w_A \cdot w_B \cdot Cov(A,B) $$

Donde $Cov(A,B)$ es la covarianza entre los activos $A$ y $B$. Alternativamente, la covarianza se puede escribir como $\sigma_{A,B}$. También es posible expresar esta fórmula en término de correlaciones. Para esto, recuerde la definición de correlación:

$$ \rho_{A,B} = \frac{Cov(A,B)}{\sigma_A \cdot \sigma_B} $$

Donde $\rho_{A,B}$ es la correlación entre los activos $A$ y $B$. Despejando la covarianza de la fórmula anterior, se tiene que:

$$ Cov(A,B) = \rho_{A,B} \cdot \sigma_A \cdot \sigma_B $$

Entonces, la fórmula de la varianza de un portafolio en términos de correlaciones es:

$$ \sigma^2_p = w_A^2 \cdot \sigma^2_A + w_B^2 \cdot \sigma^2_B + 2 \cdot w_A \cdot w_B \cdot \rho_{A,B} \cdot \sigma_A \cdot \sigma_B $$

Lo importante de esta fórmula es que la varianza de un portafolio no solo depende de la varianza de los activos, sino también de la correlación entre ellos. Por lo tanto, si se tienen dos activos con alta correlación, la varianza del portafolio será mayor que si se tienen dos activos con baja correlación.

Nótese que, implícitamente en el análisis, se asumen dos restricciones en los pesos de los activos: i) los pesos deben sumar 1 y ii) los pesos deben ser mayores o iguales a 0. Matemáticamente, esto se puede expresar como:

$$ \begin{aligned} w_A + w_B &= 1 \\ w_A, w_B &\geq 0 \end{aligned} $$

Finalmente, para construir un portafolio, uno debe considerar i) cuál es la composición de activos que genera la menor varianza y ii) cuál es la composición de activos que genera el mayor retorno ajustado por riesgo. Esto lo veremos a continuación.

Implementación

Primero, recordemos que tenemos los retornos mensuales de SPY Y de IGLB:

head(rets,2)

##                  SPY        IGLB
## Jan 2015 -0.02962922  0.05315335
## Feb 2015  0.05620460 -0.02737816

tail(rets,2)

##                 SPY        IGLB
## Nov 2019 0.03619847 0.006902604
## Dec 2019 0.02905549 0.003505400

Primero vamos a calcular los retornos promedios y desviaciones estándar históricas de los activos. Quizás también resulte ilustrativo graficarlos en el tiempo:

rets |> 
  as.data.frame() |>
  tibble::rownames_to_column(var = 'Date') |>
  # mutate Date Jan 2015, Feb 2015, etc to date
  mutate(Date = as.Date(paste0(Date, "-01"), format = "%b %Y-%d")) |>
  ggplot(aes(x = Date)) +
  geom_line(aes(y = SPY, color = "SPY", group = 1)) +
  geom_line(aes(y = IGLB, color = "IGLB", group = 1)) +
  labs(title = "Rendimientos mensuales de SPY e IGLB",
       x = "Meses",
       y = "Rendimiento") +
  scale_x_date(date_labels = "%b %Y", date_breaks = "3 month") +
  scale_y_continuous(labels = scales::percent,
                     breaks = seq(-0.1, 0.1, 0.02)
                     ) +
  scale_color_manual(values = c("SPY" = "blue", "IGLB" = "red")) +
  theme_bw()+
  theme(legend.position = "bottom", 
        axis.text.x = element_text(angle = 90, hjust = 0.5),
        text = element_text(family = 'serif', size =13),
        
        )

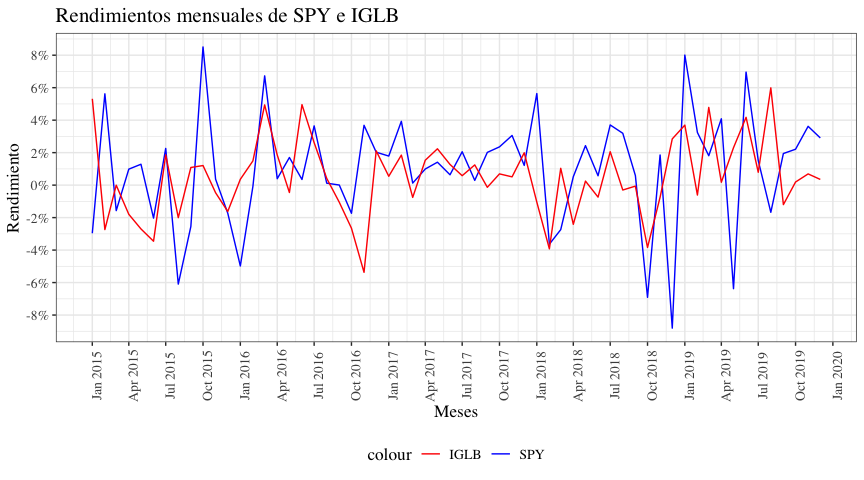
Así, parece que el activo SPY tiene un rendimiento promedio mayor que el activo IGLB, pero también tiene una mayor volatilidad, que se aprecia por la mayor amplitud de los rendimientos. Así, si tuviera que elegir entre uno de los activos o una combinación de los mismos, ¿cuál elegiría? Para responder a esta pregunta, primero vamos a calcular los retornos promedios y desviaciones estándar de los activos.

Para los retornos promedios se usa la función mean y para las desviaciones estándar se usa la función sd. Una vez calculados, se almacenan en un data.frame llamado mean_rets y std_rets, respectivamente.

meanSPY <- mean(rets$SPY)
meanIGLB <- mean(rets$IGLB)

stdSPY <- sd(rets$SPY)
stdIGLB <- sd(rets$IGLB)

mean_rets <- data.frame(meanSPY, meanIGLB)
std_rets <- data.frame(stdSPY, stdIGLB)

Así, el retorno mensual promedio es:

mean_rets

##      meanSPY    meanIGLB
## 1 0.00974469 0.004984506

Es decir, $0.9\%$ para el activo SPY y $0.5\%$ para el activo IGLB. Nótese que si anualizamos estos retornos utilizando la tasa efectiva anual:

$$ EAR = (1 + r_t)^{\frac{1}{T}} - 1 $$

Lo que es equivalente a:

$$ \begin{aligned} EAR^{SPY} &= (1 + 0.0097)^{12} - 1 \\ &= 0.1234 \\ \\ EAR^{IGLB} &= (1 + 0.0054)^{12} - 1 \\ &= 0.0615 \end{aligned}$$

Por otro lado, la desviación estándar mensual es:

std_rets

##       stdSPY    stdIGLB
## 1 0.03448889 0.02363152

Donde se comprueba que el activo SPY tiene una mayor volatilidad que el activo IGLB.

Ahora, también se necesita entender cómo se relacionan los activos entre sí. Para ello, calculamos la covarianza entre los activos SPY e IGLB. Para ello, utilizamos la función cov:

cov_rets <- cov(rets$SPY, rets$IGLB)
cov_rets

##             IGLB
## SPY 0.0001280108

También podemos graficar la relación entre los activos utilizando un diagrama de dispersión:

ggplot(data = rets, aes(x = SPY, y = IGLB)) +
  geom_point() +
  geom_smooth(method = "lm", se = FALSE, color = "blue") +
  labs(title = "Relación entre SPY e IGLB",
       x = "SPY",
       y = "IGLB")+
  theme_bw()+
  theme(text = element_text(family = 'serif', size =13),
        )

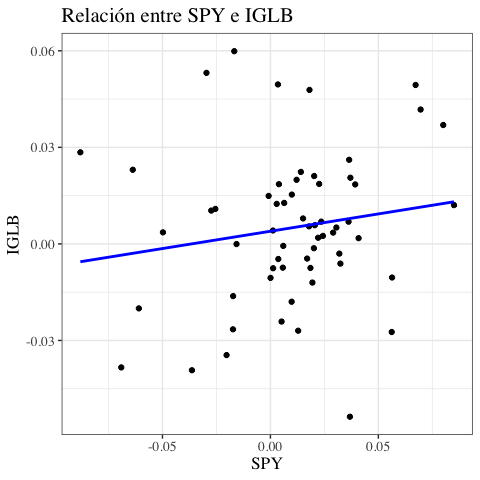
Nótese que ya tenemos todos los ingredientes para calcular el rendimiento y la varianza histórica de este portafolio. Supongamos que se invierte el $50\%$ en SPY y el $50\%$ en IGLB. Así, el rendimiento esperado del portafolio es:

$$ \begin{aligned} E(R_p) &= w_{SPY} \cdot E(R_{SPY}) + w_{IGLB} \cdot E(R_{IGLB}) \\ &= 0.5 \cdot 0.0097 + 0.5 \cdot 0.0054 \\ &= 0.00755 \end{aligned} $$

Lo que es equivalente a un $0.755\%$ mensual o un $9.45\%$ anual, aproximadamente. Por otro lado, la varianza del portafolio es:

$$\begin{align} \sigma^2_p &= w_{SPY}^2 \cdot \sigma^2_{SPY} + w_{IGLB}^2 \cdot \sigma^2_{IGLB} + 2 \cdot w_{SPY} \cdot w_{IGLB} \cdot Cov(R_{SPY}, R_{IGLB}) \\ &= 0.5^2 \cdot 0.0345^2 + 0.5^2 \cdot 0.0236^2 + 2 \cdot 0.5 \cdot 0.5 \cdot 0.00013 \\ &= 0.0005018025 \end{align}$$

Que, tomando la raíz cuadrada:

$$ \sigma_p = \sqrt{0.0005018025} = 0.0224 $$

Que, nótese es incluso menor que la volatilidad de los activos individuales ($\sigma_{SPY}=0.0345$ y $\sigma_{IGLB}=0.0236$), que es el resultado de la diversificación.

Una medida interesante para evaluar la rentabilidad de un portafolio es el coeficiente de Sharpe, que se define como:

$$ S = \frac{E(R_p) - R_f}{\sigma_p} $$

Donde $R_f$ es la tasa libre de riesgo. Supongamos que $R_f =0$. Así, el coeficiente de Sharpe es:

$$ S = \frac{0.00755}{0.0224} = 0.3370 $$

Nótese que este coeficiente se interpreta como el rendimiento adicional que se obtiene por cada unidad de riesgo adicional que se asume. Así, un coeficiente de Sharpe mayor a cero indica que el portafolio tiene un rendimiento superior al de un activo libre de riesgo, ajustado por el riesgo que se asume.

Ahora, vamos a simular 1000 portafolios con pesos secuenciales y calcular el retorno esperado, la varianza y el coeficiente de Sharpe de cada uno de ellos:

w.SPY <- seq(0, 1, by = 0.001)
w.IGLB <- 1 - w.SPY

port <- data.frame(w.SPY, w.IGLB)
head(port)

##   w.SPY w.IGLB
## 1 0.000  1.000
## 2 0.001  0.999
## 3 0.002  0.998
## 4 0.003  0.997
## 5 0.004  0.996
## 6 0.005  0.995

Ahora, calculamos el retorno esperado para cada uno de los portafolios:

port$Port.Ret <-  w.SPY * mean_rets$meanSPY + w.IGLB * mean_rets$meanIGLB

head(port)

##   w.SPY w.IGLB    Port.Ret
## 1 0.000  1.000 0.004984506
## 2 0.001  0.999 0.004989266
## 3 0.002  0.998 0.004994026
## 4 0.003  0.997 0.004998787
## 5 0.004  0.996 0.005003547
## 6 0.005  0.995 0.005008307

Ahora, calculamos la varianza de cada uno de los portafolios:

port$Port.Var <- (w.SPY^2) * std_rets$stdSPY^2 + (w.IGLB^2) * std_rets$stdIGLB^2 + 2 * w.SPY * w.IGLB * cov_rets
port$Port.Std <- sqrt(port$Port.Var)
head(port)

##   w.SPY w.IGLB    Port.Ret     Port.Var   Port.Std
## 1 0.000  1.000 0.004984506 0.0005584486 0.02363152
## 2 0.001  0.999 0.004989266 0.0005575892 0.02361333
## 3 0.002  0.998 0.004994026 0.0005567328 0.02359519
## 4 0.003  0.997 0.004998787 0.0005558794 0.02357709
## 5 0.004  0.996 0.005003547 0.0005550290 0.02355905
## 6 0.005  0.995 0.005008307 0.0005541815 0.02354106

Finalmente, calculamos el coeficiente de Sharpe de cada uno de los portafolios:

# se asume una risk-free rate de 0
rf <- 0
port$Port.Sharpe <- (port$Port.Ret - rf) / port$Port.Std
tail(port)

##      w.SPY w.IGLB    Port.Ret    Port.Var   Port.Std Port.Sharpe
## 996  0.995  0.005 0.009720889 0.001178906 0.03433520   0.2831173
## 997  0.996  0.004 0.009725649 0.001181016 0.03436591   0.2830028
## 998  0.997  0.003 0.009730410 0.001183128 0.03439663   0.2828885
## 999  0.998  0.002 0.009735170 0.001185244 0.03442737   0.2827742
## 1000 0.999  0.001 0.009739930 0.001187362 0.03445812   0.2826599
## 1001 1.000  0.000 0.009744690 0.001189483 0.03448889   0.2825458

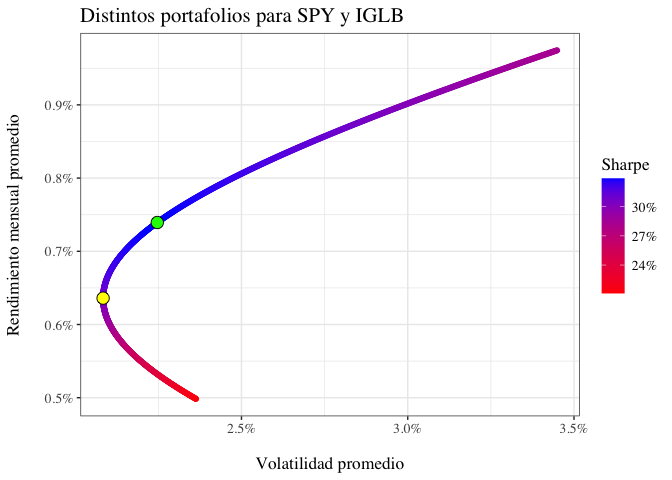
Gráficamente, los distintos portafolios se ven de la siguiente manera:

port |> 
ggplot(aes(x = Port.Std, y = Port.Ret)) +
  geom_point(aes(color = Port.Sharpe)) +
  scale_color_gradient(low = "red", high = "blue", labels = scales::percent, name = 'Sharpe') +
  scale_x_continuous(labels = scales::percent) +
  scale_y_continuous(labels = scales::percent) +
  labs(title = "Distintos portafolios para SPY y IGLB", x = "\nVolatilidad promedio", y = "Rendimiento mensual promedio\n") +
    theme_bw()+
  theme(text = element_text(family = 'serif', size =13),
        )

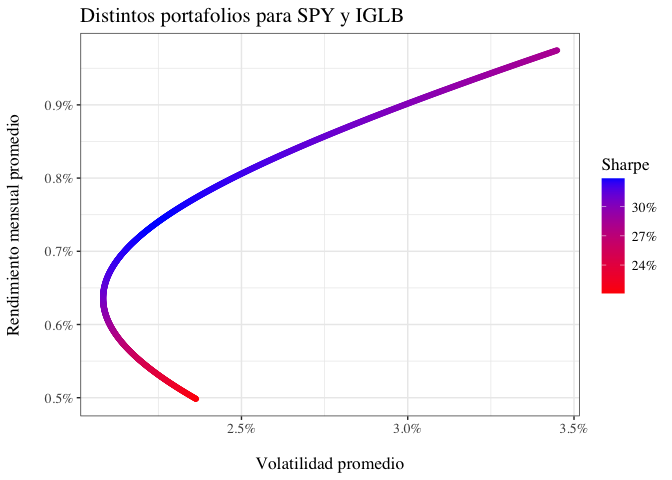
¿Cuál es el mejor portafolio?

Incialmente, identificamos el portafolio con menor varianza:

min_var_port <- port[which.min(port$Port.Std), ]
min_var_port

##     w.SPY w.IGLB    Port.Ret     Port.Var   Port.Std Port.Sharpe
## 290 0.289  0.711 0.006360199 0.0004342614 0.02083894   0.3052074

De forma gráfica, el portafolio con menor varianza se ve de la siguiente manera:

port |> 
ggplot(aes(x = Port.Std, y = Port.Ret)) +
  geom_point(aes(color = Port.Sharpe)) +
  scale_color_gradient(low = "red", high = "blue", labels = scales::percent, name = 'Sharpe\n') +
      geom_point(data = min_var_port, aes(x = Port.Std, y = Port.Ret), 
                 fill = "yellow", 
                 color = 'black',
                 pch = 21,
                 size = 4) +
  scale_x_continuous(labels = scales::percent) +
  scale_y_continuous(labels = scales::percent) +
  labs(title = "Distintos portafolios para SPY y IGLB", x = "\nVolatilidad promedio", y = "Rendimiento mensual promedio\n") +
    theme_bw()+
  theme(text = element_text(family = 'serif', size =13),
        )

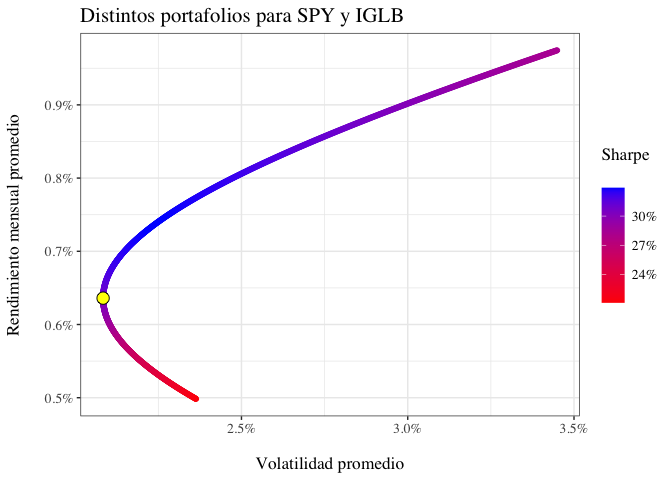
Nótese que hay un conjunto de portafolios -los que están en color rojo- en los cuales, para la misma volatilidad, se puede obtener un rendimiento mayor. Es decir, en este caso asumir más riesgo no implica necesariamente obtener un mayor rendimiento. Sin embargo, aquellos portafolios que comienzan en el portafolio de menor varianza y se desplazan hacia arriba a la derecha -aquellos que se ven en color azul- son los que se conocen como la frontera eficiente. Nótese que el coeficiente de Sharpe es mayor en la frontera eficiente, pero conforme se asume más riesgo, el coeficiente de Sharpe disminuye.

Ahora, identificamos el portafolio con mayor coeficiente de Sharpe o, lo que es lo mismo, el portafolio que es tangente a la frontera eficiente:

max_sharpe_port <- port[which.max(port$Port.Sharpe), ]
max_sharpe_port

##     w.SPY w.IGLB    Port.Ret     Port.Var   Port.Std Port.Sharpe
## 507 0.506  0.494 0.007393159 0.0005048283 0.02246839   0.3290472

Que, gráficamente:

port |> 
ggplot(aes(x = Port.Std, y = Port.Ret)) +
  geom_point(aes(color = Port.Sharpe)) +
  scale_color_gradient(low = "red", high = "blue", labels = scales::percent, name = 'Sharpe') +
  scale_x_continuous(labels = scales::percent) +
  scale_y_continuous(labels = scales::percent) +
  geom_point(data = max_sharpe_port, aes(x = Port.Std, y = Port.Ret), 
             fill = "green", 
             color = 'black',
             pch = 21,
             size = 4) +
      geom_point(data = min_var_port, aes(x = Port.Std, y = Port.Ret), 
                 fill = "yellow", 
                 color = 'black',
                 pch = 21,
                 size = 4) +
  labs(title = "Distintos portafolios para SPY y IGLB", x = "\nVolatilidad promedio", y = "Rendimiento mensual promedio\n") +
  theme_bw()+
  theme(text = element_text(family = 'serif', size =13),
        )

Dos activos: programación cuadrática

Introducción

En esta sección, se volverá a analizar el portafolio de 2 activos, pero ahora se hará uso de la técnica de programación cuadrática para encontrar el portafolio óptimo. Para resolver este problema se utilizará la función solve.QP del paquete quadprog, que permite resolver problemas de optimización cuadrática. Para esto, sin embargo, se debe plantear el problema de manera matricial.

El objetivo es demostrar que, en base a este método, ligeramente diferente al que se utilizó en la sección anterior, se obtiene el mismo portafolio óptimo. La ventaja, sin embargo, es que aunque su planteamiento requiere mayor abstracción, permitirá incluir más activos en el portafolio, lo que es tedioso de hacer de manera manual, sobre todo porque al calcular la varianza del portafolio, se deben considerar todas las combinaciones posibles de las covarianzas entre los activos.

Como esta técnica es más general, requiere también el uso de álgebra matricial, lo que puede ser un poco más complicado de entender. Por tanto, se comienza plantenado el problema de manera general y se resuelve paso a paso.

Nótese que lo que se quiere expresar en términos matriciales son las siguientes ecuaciones:

Rendimiento esperado del portafolio:

$$ E(R_p) = w_1E(R_1) + w_2 E(R_2) $$

donde $w_1$ y $w_2$ son los pesos de los activos 1 y 2, respectivamente y $E(R_1)$ y $E(R_2)$ son los rendimientos esperados de los activos 1 y 2, respectivamente.

Varianza del portafolio:

$$ \sigma_p^2 = w_1^2 \sigma_1^2 + w_2^2 \sigma_2^2 + 2w_1w_2 \sigma_{12} $$

donde $\sigma_1^2$ y $\sigma_2^2$ son las varianzas de los activos 1 y 2, respectivamente, y $\sigma_{12}$ es la covarianza entre los activos 1 y 2.

Restricciones:

En primer lugar, se tiene que la suma de los pesos de los activos 1 y 2 debe ser igual a 1:

$$ w_1 + w_2 = 1 $$

Además, los pesos de los activos 1 y 2 deben ser mayores o iguales a 0:

$$ w_1, w_2 \geq 0 $$

Enfoque matricial para el portafolio de 2 activos

Para escalar el análisis y luego utilizarlo en el caso de múltiples activos de elección, se debe expresar el problema en formato matricial. Eso es lo que se realiza en esta parte.

Valor esperado del portafolio

En primer lugar, se pueden expresar los pesos de los activos 1 y 2 en un vector de pesos:

$$ \mathbf{w} = \begin{pmatrix} w_1 \\ w_2 \end{pmatrix} $$

Sin embargo, esta notación no se limita a dos activos, sino que se puede extender a $n$ activos.

Por otra parte, los rendimientos esperados de los activos 1 y 2 se pueden expresar en un vector de rendimientos esperados. Nótese que, sin pérdida de generalidad y para simplificar la notación, se expresarán los rendimientos esperados sin el operador de la esperanza matemática, es decir, $E(R_i) \equiv R_i$.

$$ \boldsymbol{R} = \begin{pmatrix} R_1 \\ R_2 \end{pmatrix} $$

Igual que en el caso anterior, esta notación se puede extender al rendimiento de $n$ activos.

Entonces, el rendimiento esperado del portafolio es:

$$ \begin{aligned} R_p &= \mathbf{w}^\top ,\boldsymbol{R} \\ \\ &= \begin{pmatrix} w_1 & w_2 \end{pmatrix} \begin{pmatrix} R_1 \\ R_2 \end{pmatrix} \\ \\ &= w_1,R_1 + w_2,R_2. \end{aligned} $$

Varianza del portafolio

Por otra parte, la varianza del portafolio se puede expresar en términos de la matriz de covarianza de los activos 1 y 2, que se denotará como $\Sigma$:

$$ \Sigma = \begin{pmatrix} \sigma_1^2 & \sigma_{12} \\ \sigma_{21} & \sigma_2^2 \end{pmatrix} $$

donde $\sigma_1^2$ y $\sigma_2^2$ son las varianzas de los activos 1 y 2, respectivamente, $\sigma_{12}$ es la covarianza entre el rendimiento de los activos 1 y 2 y $\sigma_{21}$ es la covarianza entre los activos 2 y 1. Nótese que $\sigma_{12}=\sigma_{21}$.

Para llegar a la expresión de la varianza del portafolio, se debe post-multiplicar la matriz de covarianza por el vector de pesos y luego pre-multiplicar el vector de pesos transpuesto por el resultado anterior:

$$ \begin{aligned} \sigma_p^2 &= \mathbf{w}^\top ,\Sigma ,\mathbf{w} \\ \\ &= \begin{pmatrix} w_1 & w_2 \end{pmatrix} \begin{pmatrix} \sigma_1^2 & \sigma_{12} \\ \sigma_{21} & \sigma_2^2 \end{pmatrix} \begin{pmatrix} w_1 \\ w_2 \end{pmatrix} \\ \\ &= w_1^2 \sigma_1^2 + w_2^2 \sigma_2^2 + 2w_1w_2 \sigma_{12}. \end{aligned} $$

¿Cómo se llega a esta expresión? Se puede hacer la multiplicación paso a paso, utilizando además el hecho de que $\sigma_{12}=\sigma_{21}$:

$$ \sigma_p^2 = \begin{pmatrix} w_1 & w_2 \end{pmatrix} \begin{pmatrix} \sigma_1^2 & \sigma_{12} \\ \sigma_{12} & \sigma_2^2 \end{pmatrix} \begin{pmatrix} w_1 \\ w_2 \end{pmatrix} $$

$$ = \begin{pmatrix} w_1 & w_2 \end{pmatrix} \begin{pmatrix} w_1\sigma_1^2 + w_2\sigma_{12} \\ w_1\sigma_{12} + w_2\sigma_2^2 \end{pmatrix} $$

$$ \begin{aligned} \sigma_p^2 &= w_1^2\sigma_1^2 + w_1w_2\sigma_{12} + w_2w_1\sigma_{12} + w_2^2\sigma_2^2 \\above &= w_1^2\sigma_1^2 + w_2^2\sigma_2^2 + 2w_1w_2\sigma_{12} \end{aligned} $$

Restricciones

En cuanto a las restricciones, se pueden expresar en forma matricial de la siguiente manera:

$$ \begin{aligned} \begin{pmatrix} 1 & 1 \end{pmatrix} \begin{pmatrix} w_1 \\ w_2 \end{pmatrix} &= 1 \\ \\ \begin{pmatrix} -1 & 0 \\ 0 & -1 \end{pmatrix} \begin{pmatrix} w_1 \\ w_2 \end{pmatrix} &\leq \begin{pmatrix} 0 \\ 0 \end{pmatrix} \end{aligned} $$

Problema de optimización

Entonces, el problema de optimización se puede expresar de la siguiente manera:

$$ \begin{aligned} \min_{\mathbf{w}} &\quad \mathbf{w}^\top ,\Sigma ,\mathbf{w} \\ \\ \text{sujeto a} &\quad \mathbf{w}^\top ,\boldsymbol{R} \geq R_p^* \\ \\ &\quad \begin{pmatrix} 1 & 1 \end{pmatrix} \begin{pmatrix} w_1 \\ w_2 \end{pmatrix} = 1 \\ \\ &\quad \begin{pmatrix} -1 & 0 \\ 0 & -1 \end{pmatrix} \begin{pmatrix} w_1 \\ w_2 \end{pmatrix} \leq \begin{pmatrix} 0 \\ 0 \end{pmatrix} \end{aligned} $$

Nótese que contrario a la aplicación manual de la optimización, en esta formulación se está minimizando la varianza del portafolio sujeto a un rendimiento mínimo, $R_p^*$ en lugar de maximizar el coeficiente de Sharpe.

Programación cuadrática

En su forma canónica, un problema de programación cuadrática (QP) se puede expresar de la siguiente manera:

$$ \begin{aligned} \min_{\mathbf{x}} &\quad \frac{1}{2} \mathbf{x}^\top , Q , \mathbf{x} + \mathbf{c}^\top ,\mathbf{x} \\ \\ \text{sujeto a} &\quad \mathbf{A} ,\mathbf{x} = \mathbf{b} \\ \\ &\quad \mathbf{G} ,\mathbf{x} \leq \mathbf{h} \end{aligned} $$

Donde $Q$ es una matriz semidefinida positiva, $\mathbf{x}$ es el vector objetivo y $\mathbf{c}$ es un término lineal o de penalización. Nótese que, conjuntamente, $\mathbf{A} ,\mathbf{x} = \mathbf{b}$ representa las restricciones de igualdad, siendo $\mathbf{A}$ una matriz y $\mathbf{b}$ un vector con los valores que deben alcanzarse) Por otra parte, $\mathbf{G} ,\mathbf{x} \leq \mathbf{h}$ representa las restricciones de desigualdad, siendo $\mathbf{G}$ una matriz y $\mathbf{h}$ un vector.

¿Cómo se puede expresar el problema de optimización de la varianza mínima sujeta a un rendimiento mínimo en forma canónica de programación cuadrática? Para ello, se puede hacer uso de la siguiente notación:

Variables de decisión Primero, renombramos la variable de decisión que, en nuestro caso, son los pesos de los activos, representados por $\mathbf{w}$.

$$ \begin{aligned} \mathbf{x} &= \mathbf{w} \end{aligned} $$

Matriz de varianza-covarianza

La matriz de varianza-covarianza, $\Sigma$, es una matriz simétrica y semidefinida positiva, por lo que se puede expresar como:

$$ \begin{aligned} Q &= 2\Sigma \end{aligned} $$

El factor $2$ se incluye para que la expresión pueda simplificarse con el término $\frac{1}{2}$ en la función objetivo.

Término lineal En este caso, no hay término lineal, por lo que $\mathbf{c} = \mathbf{0}$.
Restricciones de igualdad

Se tienen $2$ restricciones de igualdad, a saber, que los pesos de los activos suman $1$ y que el retorno del portafolio debe alcanzar un retorno objetivo, por lo que $\mathbf{A}$ es una matriz con dos filas y dos columnas. Por su parte, $\mathbf{b}$ es un vector columna con dos filas. Matemáticamente:

$$ \begin{aligned} \mathbf{A} &= \begin{pmatrix} 1 & 1 \\ R_1 & R_2 \end{pmatrix} \\ \\ \mathbf{b} &= \begin{pmatrix} 1 \\ R_p^* \end{pmatrix} \end{aligned} $$

Así, expresamos las restricciones de igualdad como $\mathbf{A} ,\mathbf{x} = \mathbf{b}$.

Restricciones de desigualdad

Se tienen $2$ restricciones de desigualdad, a saber, que los pesos de los activos sean mayores o iguales a $0$. Por lo tanto, $\mathbf{G}$ es una matriz con dos filas y dos columnas. Por su parte, $\mathbf{h}$ es un vector columna con dos filas. Matemáticamente:

$$ \begin{aligned} \mathbf{G} &= \begin{pmatrix} -1 & 0 \\ 0 & -1 \end{pmatrix} \\ \\ \mathbf{h} &= \begin{pmatrix} 0 \\ 0 \end{pmatrix} \end{aligned} $$

Así, expresamos las restricciones de desigualdad como $\mathbf{G} ,\mathbf{x} \leq \mathbf{h}$.

Uniendo todo lo anterior, el problema de optimización de la varianza mínima sujeta a un rendimiento mínimo se puede expresar en forma canónica de programación cuadrática de la siguiente manera:

$$ \begin{aligned} \min_{\mathbf{w}} &\quad \frac{1}{2} \mathbf{w}^\top Q \mathbf{w} = \frac{1}{2} \mathbf{w}^\top (2\Sigma) \mathbf{w} = \mathbf{w}^\top \Sigma \mathbf{w}, \\ \text{sujeto a} &\quad A \mathbf{w} = \mathbf{b}, \quad G \mathbf{w} \leq \mathbf{h}. \end{aligned} $$

Donde:

$$ Q = 2\Sigma, \quad \mathbf{c} = \mathbf{0} \\ $$

$$ A = \begin{pmatrix}1 & 1 \\ R_1 & R_2\end{pmatrix}, \quad \mathbf{b} = \begin{pmatrix}1 \\ R_p^*\end{pmatrix} $$

$$ G = \begin{pmatrix}-1 & 0 \\ 0 & -1\end{pmatrix}, \quad \mathbf{h} = \begin{pmatrix}0 \\ 0\end{pmatrix} $$

Implementación

Como se indicaba al inicio de la sección, se puede resolver el problema de optimización de la varianza mínima sujeta a un rendimiento mínimo utilizando la función solve.QP del paquete quadprog. Para ello, se debe instalar el paquete y cargarlo en la sesión de trabajo:

install.packages("quadprog")

Una vez instalado, se puede cargar el paquete:

library(quadprog)

Particularmente, se utilizará la función solve.QP, por lo que es importante familirizarse bien con ella y los argumenos que toma. Para ello, incialmente miramos la documentación:

?quadprog::solve.QP

Lo que nos devuelve la siguiente información:

Es decir, la función quadprog::solve.QP espera realmente la información de la siguiente manera:

$$ \begin{aligned} \text{min} \quad & -\mathbf{d}^\top \mathbf{b} + \tfrac12 \mathbf{b}^\top \mathbf{D} \mathbf{b} \\ \text{s.t.} \quad & \mathbf{A}^\top \mathbf{b} \ge \mathbf{b_0} \end{aligned} $$

Entonces, necesitamos definir los siguientes elementos:

Dmat ($\mathbf{D}$): Es una matriz positiva semidefinida de tamaño $n \times n$ que representa la matriz $Q$ del planteamiento canónico o la matriz $2,\Sigma$.
dvec ($\mathbf{d}$) : vector de tamaño $n$ que representa el vector $\mathbf{c}$. En este caso, $\mathbf{c} = \mathbf{0}$.
Amat: matriz de tamaño $m \times n$ que representa la matriz $A$.
bvec ($\mathbf{b}$): vector de tamaño $n$ que representa el vector objetivo o los pesos del portafolio, $\mathbf{b} = \mathbf{w}$.
meq: número de restricciones de igualdad.
factorized: valor lógico que indica si la matriz Dmat está factorizada.

Nótese que solve.QP no permite restricciones de desigualdad, por lo que se deben transformar en restricciones de igualdad. Por tanto, la matriz $\mathbf{G}$ y el vector $\mathbf{h}$ se deben incorporar en la matriz $\mathbf{A}$ y el vector $\mathbf{b}$, respectivamente. Posteriormente, con el argumento meq se indica el número de restricciones de igualdad que, en este caso, es $2$.

Entonces, para crear estas matrices debemos reorganizar los datos construidos previamente.

Primero, se debe recordar que, previamente, se había calculado rets, un data.frame con los retornos mensuales de los activos SPY (acciones) y IGLB (bonos):

head(rets)

##                  SPY          IGLB
## Jan 2015 -0.02962922  0.0531533456
## Feb 2015  0.05620460 -0.0273781648
## Mar 2015 -0.01570556 -0.0000474542
## Apr 2015  0.00983389 -0.0179675606
## May 2015  0.01285580 -0.0269743998
## Jun 2015 -0.02031166 -0.0345466505

Para poder utilizar esta información en la función solve.QP, se deben expresar los retornos en forma de matricial:

mat.ret <- matrix(rets, nrow=nrow(rets))
colnames(mat.ret) <- c("SPY", "IGLB")
head(mat.ret)

##              SPY          IGLB
## [1,] -0.02962922  0.0531533456
## [2,]  0.05620460 -0.0273781648
## [3,] -0.01570556 -0.0000474542
## [4,]  0.00983389 -0.0179675606
## [5,]  0.01285580 -0.0269743998
## [6,] -0.02031166 -0.0345466505

Adicionalmente, es posible calcular los rendimientos esperados de los activos, que son los promedios de los retornos mensuales y que nos servirán más adelante:

avg.ret <- matrix(apply(mat.ret, 2, mean))
colnames(avg.ret) <- paste("Avg.Ret")
rownames(avg.ret) <- paste(c("SPY","IGLB"))
avg.ret

##          Avg.Ret
## SPY  0.009744690
## IGLB 0.004984506

Ahora, se deben definir los elementos de la función solve.QP. Iniciamos con la matriz Dmat que, como se mencionó anteriormente, es la matriz $Q$ de la expresión canónica o la expresión $2,\Sigma$, eso es, la matriz de variances-covarianzas multiplicada por $2$. Matricialmente:

$$ \begin{aligned} \mathbf{D} &= 2,\Sigma \end{aligned} $$

Por lo tanto, la matriz Dmat es:

vcov <- cov(mat.ret)
Dmat <- 2 * vcov
Dmat

##               SPY         IGLB
## SPY  0.0023789668 0.0002560217
## IGLB 0.0002560217 0.0011168972

El vector dvec es un vector de ceros (porque no hay penalizaciones lineales en la función objetivo, es decir, $\mathbf{c} = \mathbf{0}$). Lo único es que se debe tener cuidado con la longitud del vector, que debe ser igual al número de columnas de la matriz mat.ret:

dvec <- rep(0, ncol(mat.ret))
dvec

## [1] 0 0

En el caso anterior se utilizó la función base::rep que replica el primer argumento, $0$, el número de veces que indique el segundo argumento, ncol(mat.ret). Además, se utiliza base::ncol para obtener el número de columnas de la matriz mat.ret.

Por otro lado, la matriz Amat y el vector bvec se definen a partir de las restricciones de igualdad, a saber, que los pesos sumen uno y que el rendimiento esperado sea mayor o igual a un valor objetivo. Sin embargo, como se mencionó anteriormente, también se deberán agregar las restricciones de desigualdad que, en este caso, indican que la proporción de nuestro presupuesto que se dedican a los distintos activos sean mayores o iguales a cero.

Por tanto, en la forma canónica la matriz $\mathbf{A}$ sería:

$$ \begin{aligned} \mathbf{A} &= \begin{pmatrix}1 & 1 \\ R_1 & R_2\end{pmatrix} \end{aligned} $$

Sin embargo, para utilizarla en la función solve.QP se debe agregar una fila a la matriz $\mathbf{A}$ por cada activo adiciona que se esté considerando, indicando que los pesos sean mayores o iguales a cero. Por lo tanto, en el caso particular, la matriz $\mathbf{A}$ se define como:

$$ \begin{aligned} \mathbf{A} &= \begin{pmatrix}1 & 1 \\ R_1 & R_2 \\ 1 & 0 \\ 0 & 1\end{pmatrix} \end{aligned} $$

Como se mencionó anteriormente, con el argumento meq = 2 se indicará que las dos primeras filas de la matriz Amat son restricciones de igualdad.

Finalmente, de la forma que se ha implementado quadprog::solve.QP, la matriz $\mathbf{A}$ debe ser transpuesta, $\mathbf{A}^\top$, es decir:

$$ \begin{aligned} \mathbf{A}^\top &= \begin{pmatrix}1 & R_1 & 1 & 0 \\ 1 & R_2 & 0 & 1\end{pmatrix} \end{aligned} $$

Que, en código, se define como:

Amat <- cbind(rep(1, ncol(mat.ret)), 
              avg.ret,
              diag(1, nrow = ncol(mat.ret)))
Amat

##            Avg.Ret    
## SPY  1 0.009744690 1 0
## IGLB 1 0.004984506 0 1

Donde utilizando base::cbind primero se agrega una columna de unos ($1$s) con una cantidad de valores como activos se estén analizando. Esto representa la restricción de que la sumatoria de todos los pesos debe ser igual a $1$. Luego se agrega el vector avg.ret, que son los retornos mensuales promedio de los activos, que es un dato estimado. Finalmente, se agrega una matriz identidad de tamaño $n \times n$ donde $n$ es el número de activos. Esta matriz identidad representará las restricciones de desigualdad, es decir, que los pesos de cada activo sean mayores o iguales a cero.

Finalmente, se debe definir el vector bvec ($\mathbf{b_0}$) que es el vector de restricciones de igualdad y desigualdad. En este caso, se debe indicar que la sumatoria de los pesos sea igual a uno y que el rendimiento esperado sea igual a un valor objetivo. Adicionalmente, como se mencionó anteriormente, se deben agregar las restricciones de desigualdad que indican que los pesos de cada activo sean mayores o iguales a cero. Matemáticamente, el vector bvec se define como:

$$ \begin{aligned} \mathbf{b_0} &= \begin{pmatrix}1 \\ R_p^* \\ 0 \\ 0\end{pmatrix} \end{aligned} $$

Donde $R_p^*$ es el rendimiento esperado que se desea obtener.

Se debe recordar que, el ejercicio de programación cuadrática implica minimizar la varianza del portafolio para distintos retornos objetivos. En este sentido, se utilizará un rango de valores de rendimiento objetivo, por lo que se definirá un vector de rendimientos, tgt.ret, que va desde el rendimiento esperado mínimo hasta el rendimiento esperado máximo. Por lo tanto, el vector bvec se define como:

min.ret <- min(avg.ret)
max.ret <- max(avg.ret)

increments <- 1000

tgt.ret <- seq(min.ret, max.ret, length = increments)

head(tgt.ret)

## [1] 0.004984506 0.004989271 0.004994036 0.004998801 0.005003566 0.005008331

El cual se puede interpretar como un vector de rendimientos esperados que se desean obtener. En este caso, se utilizarán {r} increments valores de rendimiento esperado que van desde el rendimiento esperado mínimo hasta el rendimiento esperado máximo. Este vector podría expandirse o contraerse dependiendo de la cantidad de valores que se deseen analizar.

Finalmente, se necesitan crear dos vectores adicionales que almacenen los resultados de la optimización. El primero, tgt.sd, almacenará los distintos valores de desviación estándar obtenidos para cada rendimiento esperado. El segundo, wgt, almacenará los pesos óptimos de cada activo para cada rendimiento esperado. Ambos vectores se inicializan con ceros.

tgt.sd <- rep(0, length = increments)
wgt <- matrix(0, nrow = increments, ncol = ncol(mat.ret))

Ahora se procederá a realizar la optimización de la cartera para cada uno de los rendimientos esperados. Para ello, se utilizará un bucle for que recorrerá cada uno de los valores de rendimiento esperado. En cada iteración, se realizará la optimización de la cartera utilizando la función quadprog::solve.QP y se almacenarán los resultados en los vectores tgt.sd y wgt.

for (i in 1:increments) {
  bvec <- c(1, tgt.ret[i], rep(0, ncol(mat.ret)))
  sol <- quadprog::solve.QP(Dmat = Dmat, 
                            dvec = dvec,
                            Amat = Amat, 
                            bvec = bvec, 
                            meq = 2)
  tgt.sd[i] <- sqrt(sol$value)
  wgt[i, ] <- sol$solution
}

Ahora, vamos a crear un data.frame que contenga los resultados obtenidos. Para ello, se utilizará la función base::data.frame que permitirá crear un data.frame con los vectores tgt.ret, tgt.sd y wgt. Finalmente, se renombrarán las columnas del data.frame para que sean más descriptivas.

results <- data.frame(tgt.ret, tgt.sd, round(wgt,8))
colnames(results)[c(3,4)] <- c("w.SPY", "w.IGLB")
head(results)

##       tgt.ret     tgt.sd      w.SPY   w.IGLB
## 1 0.004984506 0.02363152 0.00000000 1.000000
## 2 0.004989271 0.02361331 0.00100100 0.998999
## 3 0.004994036 0.02359515 0.00200200 0.997998
## 4 0.004998801 0.02357704 0.00300300 0.996997
## 5 0.005003566 0.02355898 0.00400400 0.995996
## 6 0.005008331 0.02354097 0.00500501 0.994995

Ahora, se procederá a graficar los resultados obtenidos. Para ello, se utilizará la función ggplot2::ggplot que permitirá crear un gráfico para todas las combinaciones de retorno y riesgo de cada portafolio. En este caso, se graficará la desviación estándar en el eje $x$ y el rendimiento esperado en el eje $y$. Adicionalmente, se graficarán los puntos que representan los distintos portafolios obtenidos y se unirán con una línea para visualizar la frontera eficiente, que se encontrará en el conjunto de puntos que están por encima del portafolio de menor varianza:

results |> 
ggplot(aes(x = tgt.sd, y = tgt.ret)) +
  geom_point(aes(color = w.SPY)) +
  scale_color_gradient(low = "red", high = "blue", labels = scales::percent, name = '% in SPY\n') +
  scale_x_continuous(labels = scales::percent) +
  scale_y_continuous(labels = scales::percent) +
  labs(title = "Distintos portafolios para SPY y IGLB", x = "\nVolatilidad promedio", y = "Rendimiento mensual promedio\n") +
    theme_bw()+
  theme(text = element_text(family = 'serif', size =13),
        )

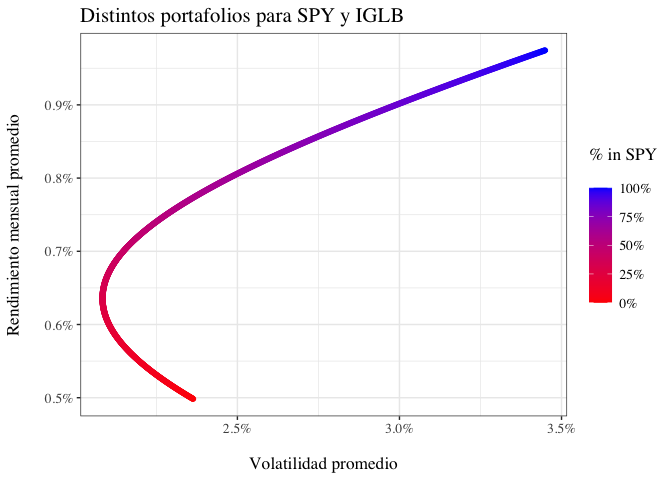
Entonces, ¿cuál es el portafolio de menor varianza?

min.sd.portfolio <- results[which.min(results$tgt.sd), ]
min.sd.portfolio

##         tgt.ret     tgt.sd     w.SPY    w.IGLB
## 289 0.006356811 0.02083893 0.2882883 0.7117117

¿Cuál es el portafolio de mayor rendimiento ajustado por riesgo?

max.sharpe.portfolio <- results[which.max(results$tgt.ret/ results$tgt.sd ), ]
max.sharpe.portfolio

##        tgt.ret     tgt.sd     w.SPY    w.IGLB
## 507 0.00739557 0.02247571 0.5065065 0.4934935

$n$ activos: programación cuadrática

En el caso anterior, se analizó la optimización de un portafolio de dos activos. Sin embargo, en la práctica, los inversionistas suelen tener portafolios con más de dos opciones de inversión. En este sentido, se puede extender el análisis de la optimización de portafolios a un número arbitrario de activos. Para ello, se debe realizar una serie de modificaciones en el código anterior.

En lo que sigue, se volverá a realizar el análisis desde el inicio.

Cargar datos

En primer lugar, cargamos los activos que se desean analizar. Se utiliza el paquete quantmod para descargar los precios de cierre ajustados de los activos. En este caso, se analizarán los activos:

Procter & Gamble Company (PG)
Berkshire Hathaway (BRK-B)
Pfizer (PFE)
Goldman Sachs Group (GS)
Coca-Cola Company (KO)
Apple (AAPL)

Entonces:

tickers <- c("PG", "BRK-B", "PFE", "GS", "KO", "AAPL")

quantmod::getSymbols(tickers, from = "2018-12-31", to = "2024-12-31")

## [1] "PG"    "BRK-B" "PFE"   "GS"    "KO"    "AAPL"

head(AAPL)

##            AAPL.Open AAPL.High AAPL.Low AAPL.Close AAPL.Volume AAPL.Adjusted
## 2018-12-31   39.6325   39.8400  39.1200    39.4350   140014000      37.62425
## 2019-01-02   38.7225   39.7125  38.5575    39.4800   148158800      37.66718
## 2019-01-03   35.9950   36.4300  35.5000    35.5475   365248800      33.91526
## 2019-01-04   36.1325   37.1375  35.9500    37.0650   234428400      35.36308
## 2019-01-07   37.1750   37.2075  36.4750    36.9825   219111200      35.28436
## 2019-01-08   37.3900   37.9550  37.1300    37.6875   164101200      35.95698

Ahora, se procederá a obtener los rendimientos mensuales. Para ello, primero se convertirán los precios diarios a mensuales utilizando xts::to.monthly. Posteriormente, se calcularán los rendimientos mensuales utilizando quantmod::Delt.

aapl <- xts::to.monthly(AAPL)
brk.b <- xts::to.monthly(`BRK-B`)
pfe <- xts::to.monthly(PFE)
gs <- xts::to.monthly(GS)
ko <- xts::to.monthly(KO)
pg <- xts::to.monthly(PG)


rets <- cbind(quantmod::Delt(aapl$AAPL.Adjusted), 
              quantmod::Delt(brk.b$`BRK-B.Adjusted`), 
              quantmod::Delt(pfe$PFE.Adjusted), 
              quantmod::Delt(gs$GS.Adjusted), 
              quantmod::Delt(ko$KO.Adjusted), 
              quantmod::Delt(pg$PG.Adjusted))

rets <- rets[-1, ]

colnames(rets) <- tickers

head(rets)

##                   PG        BRK-B         PFE           GS           KO
## Jan 2019  0.05515397  0.006660793 -0.01899816  0.185333754  0.016473306
## Feb 2019  0.04477689 -0.020628541  0.02120158 -0.002604335 -0.057968300
## Mar 2019  0.09702542 -0.002036779 -0.02029976 -0.023945108  0.042547380
## Apr 2019  0.05643585  0.078749601 -0.04379587  0.072556000  0.046948478
## May 2019 -0.12421283 -0.089013003  0.03147647 -0.109787757  0.001426383
## Jun 2019  0.13051897  0.079779152  0.04335262  0.121157514  0.044524757
##                 AAPL
## Jan 2019  0.05780046
## Feb 2019  0.02156099
## Mar 2019  0.05580929
## Apr 2019  0.03057847
## May 2019 -0.03352765
## Jun 2019  0.06549407

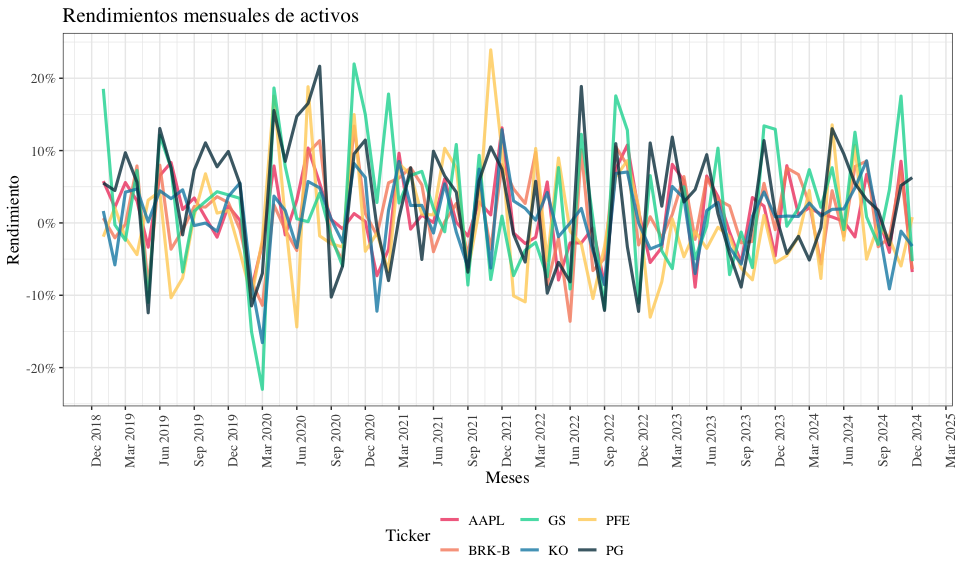
Finalmente, podemos visualizar los rendimientos mensuales de los activos:

rets |> 
  as.data.frame() |>
  tibble::rownames_to_column(var = 'Date') |>
  # mutate Date Jan 2015, Feb 2015, etc to date
  mutate(Date = as.Date(paste0(Date, "-01"), format = "%b %Y-%d")) |>
  ggplot(aes(x = Date)) +
  geom_line(aes(y = AAPL, color = "AAPL", group = 1), linewidth = 1.1, alpha = 0.8) +
  geom_line(aes(y = `BRK-B`, color = "BRK-B", group = 1), linewidth = 1.1, alpha = 0.8) +
  geom_line(aes(y = PFE, color = "PFE", group = 1), linewidth = 1.1, alpha = 0.8) +
  geom_line(aes(y = GS, color = "GS", group = 1), linewidth = 1.1, alpha = 0.8) +
  geom_line(aes(y = KO, color = "KO", group = 1), linewidth = 1.1, alpha = 0.8) +
  geom_line(aes(y = PG, color = "PG", group = 1), linewidth = 1.1, alpha = 0.8) +
  labs(title = "Rendimientos mensuales de activos",
       x = "Meses",
       y = "Rendimiento") +
  scale_x_date(date_labels = "%b %Y", date_breaks = "3 month") +
  scale_y_continuous(labels = scales::percent
                     ) +
  scale_color_manual('Ticker', values = c("AAPL" = "#ef476f", "BRK-B" = "#f78c6b", "PFE" = "#ffd166", "GS" = "#06d6a0", "KO" = "#118ab2", "PG" = "#073b4c")) +
  theme_bw()+
  theme(legend.position = "bottom", 
        axis.text.x = element_text(angle = 90, hjust = 0.5),
        text = element_text(family = 'serif', size =13),
        
        )

Optimización de portafolio

En segundo lugar, se procederá a optimizar el portafolio de los activos seleccionados. Para ello, otra vez, se necesita expresar los datos de forma matricial, tal que quadprog::solve.QP pueda resolver el problema de optimización. Esto es:

$$ \begin{aligned} \text{min} \quad & -\mathbf{d}^\top \mathbf{b} + \tfrac12 \mathbf{b}^\top \mathbf{D} \mathbf{b} \\ \text{s.t.} \quad & \mathbf{A}^\top \mathbf{b} \ge \mathbf{b_0} \end{aligned} $$

Data wrangling

Entonces, iniciamos convirtiendo los rendimientos en matrices:

mat.ret <- matrix(rets, nrow = nrow(rets))
colnames(mat.ret) <- tickers
head(mat.ret)

##               PG        BRK-B         PFE           GS           KO        AAPL
## [1,]  0.05515397  0.006660793 -0.01899816  0.185333754  0.016473306  0.05780046
## [2,]  0.04477689 -0.020628541  0.02120158 -0.002604335 -0.057968300  0.02156099
## [3,]  0.09702542 -0.002036779 -0.02029976 -0.023945108  0.042547380  0.05580929
## [4,]  0.05643585  0.078749601 -0.04379587  0.072556000  0.046948478  0.03057847
## [5,] -0.12421283 -0.089013003  0.03147647 -0.109787757  0.001426383 -0.03352765
## [6,]  0.13051897  0.079779152  0.04335262  0.121157514  0.044524757  0.06549407

Una vez con la información en el formato correcto, se procede a calcular los rendimientos esperados y la matriz de varianzas y covarianzas.

Iniciando por los rendimientos mensuales esperados:

avg.ret <- matrix(apply(mat.ret, 2, mean))
rownames(avg.ret) <- tickers
colnames(avg.ret) <- c("Avg.Ret")
avg.ret

##             Avg.Ret
## PG    0.02999118009
## BRK-B 0.01276010267
## PFE   0.00002661511
## GS    0.02317229946
## KO    0.00767418332
## AAPL  0.01168301605

Ahora calculamos la matriz de varianzas y covarianzas:

vcov <- cov(mat.ret)
vcov

##                PG       BRK-B         PFE          GS          KO        AAPL
## PG    0.006672793 0.002386728 0.002009316 0.003455244 0.001561821 0.001569067
## BRK-B 0.002386728 0.003370596 0.001511430 0.003217788 0.001814290 0.001354124
## PFE   0.002009316 0.001511430 0.005833581 0.001626770 0.001024040 0.001015396
## GS    0.003455244 0.003217788 0.001626770 0.007944929 0.002199052 0.001287051
## KO    0.001561821 0.001814290 0.001024040 0.002199052 0.002613038 0.001743099
## AAPL  0.001569067 0.001354124 0.001015396 0.001287051 0.001743099 0.002520521

A continuación se definen 1) el vector de rendimientos objetivo que será utilizado iterativamente para encontrar el portafolio óptimo y 2) los vectores de pesos óptimos y desviación estándar asociada a cada rendimiento objetivo que se utilizarán para almacenar los resultados de la optimización.

# Límites de rendimientos esperados
min.ret <- min(avg.ret)
max.ret <- max(avg.ret)

# Definir cuántos puntos se desean para la construcción de portafolios

increments <- 1000

# Crear el vector de rendimientos objetivo
tgt.ret <- seq(min.ret, max.ret, length = increments)

head(tgt.ret)

## [1] 0.00002661511 0.00005660967 0.00008660423 0.00011659879 0.00014659335
## [6] 0.00017658791

Ahora construimos los vectores de pesos óptimos y desviación estándar asociada a cada rendimiento objetivo:

# Vector de 0s para almacenar desviaciones estándar
tgt.sd <- rep(0, length = increments)

# Vector de 0s para almacenar pesos óptimos
wgt <- matrix(0, nrow = increments, ncol = ncol(mat.ret))

Ejecución del algoritmo de optimización

Ahora se cuenta con toda la información necesaria para ejecutar el algoritmo de optimización. Para ello, se utilizará la función quadprog::solve.QP que resuelve el problema de optimización cuadrática.

for (i in 1:increments){
  Dmat <- 2*vcov
  dvec <- c(rep(0, ncol(mat.ret)))
  Amat <- cbind(rep(1, ncol(mat.ret)), avg.ret,
                diag(1, nrow = ncol(mat.ret)))
  bvec <- c(1, tgt.ret[i], rep(0, ncol(mat.ret)))
  soln <- quadprog::solve.QP(Dmat, dvec, Amat, bvec, meq = 2)
  tgt.sd[i] <- sqrt(soln$value)
  wgt[i, ] <- soln$solution
}

head(tgt.sd)

## [1] 0.07637788 0.07613115 0.07588492 0.07563918 0.07539395 0.07514923

Nótese que los resultados han sido almacenados tanto en tgt.sd como en wgt, que representan las desviaciones estándar alcanzadas para cada retorno objetivo y los pesos óptimos asociados, respectivamente. Por ejemplo, estos últimos son:

# Cambiar los nombres de las columnas añadiendo un prefijo "w." a cada ticker
tickers_pesos <- paste0("w.", tickers)
colnames(wgt) <- tickers_pesos
head(round(wgt,8))

##      w.PG w.BRK-B     w.PFE w.GS       w.KO w.AAPL
## [1,]    0       0 1.0000000    0 0.00000000      0
## [2,]    0       0 0.9960779    0 0.00392210      0
## [3,]    0       0 0.9921558    0 0.00784421      0
## [4,]    0       0 0.9882337    0 0.01176631      0
## [5,]    0       0 0.9843116    0 0.01568842      0
## [6,]    0       0 0.9803895    0 0.01961052      0

Análisis de resultados

Iniciamos el análisis combinando los resultados en un solo data.frame para facilitar su manipulación y visualización:

portfolios <- data.frame(cbind(tgt.ret, tgt.sd, round(wgt,8)))

head(portfolios)

##         tgt.ret     tgt.sd w.PG w.BRK.B     w.PFE w.GS       w.KO w.AAPL
## 1 0.00002661511 0.07637788    0       0 1.0000000    0 0.00000000      0
## 2 0.00005660967 0.07613115    0       0 0.9960779    0 0.00392210      0
## 3 0.00008660423 0.07588492    0       0 0.9921558    0 0.00784421      0
## 4 0.00011659879 0.07563918    0       0 0.9882337    0 0.01176631      0
## 5 0.00014659335 0.07539395    0       0 0.9843116    0 0.01568842      0
## 6 0.00017658791 0.07514923    0       0 0.9803895    0 0.01961052      0

Finalmente se agregará una columna adicional que indique el Sharpe ratio de cada portafolio:

# Se asume una tasa libre de riesgo de 0
rf <- 0

# Calcular el Sharpe ratio
portfolios$sharpe <- (portfolios$tgt.ret - rf) / portfolios$tgt.sd

Una vez con el data frame portfolios listo, se procede a graficar la frontera eficiente de Markowitz:

portfolios |>
ggplot(aes(x = tgt.sd, y = tgt.ret)) +
  geom_point(aes(color = sharpe)) +
  scale_color_gradient(low = "red", high = "blue", labels = scales::percent, name = 'Sharpe') +
  scale_x_continuous(labels = scales::percent) +
  scale_y_continuous(labels = scales::percent) +
  labs(title = "Distintos portafolios de Activos", x = "\nVolatilidad promedio", y = "Rendimiento mensual promedio\n") +
  theme_bw()+
  theme(text = element_text(family = 'serif', size =13),
        )

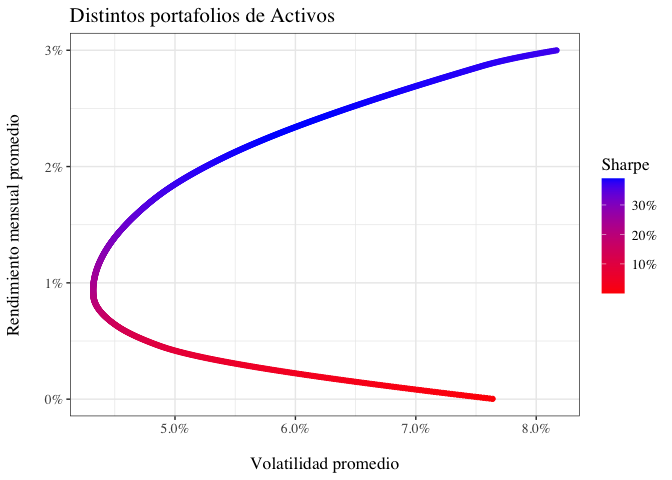
Entonces, nos interesan dos portafolios:

El portafolio con menor volatilidad
El portafolio con mayor Sharpe ratio

Para encontrar estos portafolios, se procede a filtrar el data frame portfolios:

# Portafolio con menor volatilidad
min_vol_port <- portfolios[which.min(portfolios$tgt.sd),]
min_vol_port

##         tgt.ret     tgt.sd       w.PG   w.BRK.B     w.PFE w.GS     w.KO
## 312 0.009354923 0.04320431 0.01769955 0.1740216 0.1545207    0 0.259033
##        w.AAPL    sharpe
## 312 0.3947251 0.2165275

Ahora, el portafolio con mayor Sharpe ratio:

# Portafolio con mayor Sharpe ratio
max_sharpe_port <- portfolios[which.max(portfolios$sharpe),]
max_sharpe_port

##        tgt.ret    tgt.sd      w.PG w.BRK.B w.PFE     w.GS w.KO    w.AAPL
## 782 0.02345237 0.0601524 0.5369123       0     0 0.168807    0 0.2942807
##        sharpe
## 782 0.3898825

Nótese que el portafolio con mayor Sharpe ratio, que implica un rendimiento esperado mensual de $2.34\%$ (equivalente a $32.07\%$ anual) y una volatilidad de $0.06\%$, está compuesto por:

Activo	Peso
Procter & Gamble (`PG`)	$53.69\%$
Berkshire Hathaway (`BRK-B`)	$0\%$
Pfizer (`PFE`)	$0\%$
Goldman Sachs (`GS`)	$16.88\%$
Coca-Cola (`KO`)	$0\%$
Apple (`AAPL`)	$29.43\%$

Gráficamente:

# Gráfico con los portafolios seleccionados
portfolios |>
ggplot(aes(x = tgt.sd, y = tgt.ret)) +
  geom_point(aes(color = sharpe)) +
  geom_point(data = min_vol_port, aes(x = tgt.sd, y = tgt.ret), 
             fill = "yellow", 
             color = 'black',
             pch= 21,
             size = 5) +
  geom_point(data = max_sharpe_port, aes(x = tgt.sd, y = tgt.ret), 
             fill = "green", 
             color = 'black',
             pch= 21,
             size = 5) +
  scale_color_gradient(low = "red", high = "blue", labels = scales::percent, name = 'Sharpe') +
  scale_x_continuous(labels = scales::percent) +
  scale_y_continuous(labels = scales::percent) +
  labs(title = "Distintos portafolios de Activos", x = "\nVolatilidad promedio", y = "Rendimiento mensual promedio\n") +
  theme_bw()+
  theme(text = element_text(family = 'serif', size =13),
        )

Donde el portafolio óptimo (mayor retorno ajustado al riesgo) se representa con el punto de color verde.

Portafolio de mercado: S&P 500

Ahora que se ha construido la herramienta, sería interesante construir un portafolio de mercado. Para esto, se analizarán las $500$ compañías que componen el índice S&P 500. Para ello, se extraerán los datos de la página web stockanalysis.com. Para ello se utilizará el paquete rvest que permite extraer información de páginas web.

library(rvest)

Para extraer la información de la página web, se debe leer la misma y extraer la tabla que contiene la información de las compañías. Posteriormente, se limpiarán los nombres de las columnas.

url <- "https://stockanalysis.com/list/sp-500-stocks/"

# Read the webpage
webpage <- read_html(url)

# Extract the table containing the stocks
sp500_table <- webpage %>%
  html_element("table") %>%  # Locate the first table
  html_table(fill = TRUE)    # Convert it into a dataframe

# Clean column names (optional)
colnames(sp500_table) <- c("Rank", "Ticker", "Company", "Market_Cap", "Stock_Price", "Growth", "Revenue")

# Cambiar puntos en Ticker por guiones
sp500_table$Ticker <- gsub("\\\.", "-", sp500_table$Ticker)

# Display first few rows
head(sp500_table)

## # A tibble: 6 × 7
##    Rank Ticker Company               Market_Cap Stock_Price Growth Revenue
##   <int> <chr>  <chr>                 <chr>      <chr>       <chr>  <chr>  
## 1     1 AAPL   Apple Inc.            3,419.77B  227.65      0.12%  395.76B
## 2     2 NVDA   NVIDIA Corporation    3,271.13B  133.57      2.87%  113.27B
## 3     3 MSFT   Microsoft Corporation 3,064.44B  412.22      0.60%  261.80B
## 4     4 AMZN   Amazon.com, Inc.      2,470.75B  233.14      1.74%  637.96B
## 5     5 GOOG   Alphabet Inc.         2,282.58B  188.20      0.57%  350.02B
## 6     6 GOOGL  Alphabet Inc.         2,273.07B  186.47      0.61%  350.02B

Nótese que solo se necesitan los tickers de las compañías, por lo que se extraerán de la tabla anterior:

tickers_sp500 <- sp500_table$Ticker
# remove 'GOOG' que está casi perfectamente correlacionado con 'GOOGL'
tickers_sp500 <- tickers_sp500[-which(tickers_sp500 == "GOOG")]
head(tickers_sp500)

## [1] "AAPL"  "NVDA"  "MSFT"  "AMZN"  "GOOGL" "META"

Ahora, se procederá a descargar los datos de los activos del S&P 500. Para ello, se utilizará la función quantmod::getSymbols que permite descargar los precios de cierre ajustados de los activos. En este caso, se descargarán los datos desde el $1$ de enero de $2023$ hasta la fecha actual:

activos <- list()

for (ticker in tickers_sp500){
  tryCatch({
    activos[[ticker]] <- quantmod::getSymbols(ticker, from = "2023-01-01", to = Sys.Date(), auto.assign = FALSE)
  }, error = function(e) {
    print(paste("Error en ticker", ticker))
  })
}

Finalmente se procederá a realizar la optimización del portafolio de mercado. Para ello, se utilizará la misma metodología que se utilizó anteriormente. Sin embargo, se debe tener en cuenta que se deben eliminar los activos que no tengan información disponible.

get_monthly_returns <- function(ticker) {
  if (!is.null(activos[[ticker]])) {
    data_xts <- activos[[ticker]]  # Extraer datos descargados
    monthly_data <- to.monthly(data_xts, indexAt = "lastof")  # Convertir a mensual
    monthly_rets <- Delt(Cl(monthly_data), type = 'arithmetic')  # Calcular rendimientos sobre precios de cierre
    colnames(monthly_rets) <- ticker
    return(monthly_rets[-1, ])  # Eliminar la primera fila NA
  } else {
    return(NULL)
  }
}

# Aplicar la función a todos los activos
monthly_returns_list <- lapply(names(activos), get_monthly_returns)

# Convertir lista a data frame
monthly_returns_df <- do.call(merge, monthly_returns_list)

# Combinar todos los retornos en un solo dataframe
rets_sp500 <- do.call(cbind, monthly_returns_list)

# Convertir a matriz base R
mat.ret_sp500 <- matrix(rets_sp500, nrow = nrow(rets_sp500))
colnames(mat.ret_sp500) <- names(activos)

# Contar numero de NAs por columna
nas <- colSums(is.na(mat.ret_sp500))
names(nas) <- names(activos)

# Eliminar activos con NAs
mat.ret_sp500 <- mat.ret_sp500[, which(nas == 0)]

# Calcula los rendimientos esperados with na.rm = TRUE

avg.ret_sp500 <- matrix(apply(mat.ret_sp500, 2, mean, na.rm = TRUE))

rownames(avg.ret_sp500) <- colnames(mat.ret_sp500)
colnames(avg.ret_sp500) <- c("Avg.Ret")

# Calcula la matriz de varianzas y covarianzas
vcov_sp500 <- cov(mat.ret_sp500)


# Definir el rango de rendimientos objetivo
min_ret <- 0 # min(avg.ret_sp500)
max_ret <- max(avg.ret_sp500)

increments <- 100

tgt.ret_sp500 <- seq(min_ret, max_ret, length.out = increments)

# Vector de 0s para almacenar desviaciones estándar
tgt.sd_sp500 <- rep(0, length = increments)

# Vector de 0s para almacenar pesos óptimos
wgt_sp500 <- matrix(0, nrow = increments, ncol = ncol(mat.ret_sp500))


# Cambiar los nombres de las columnas añadiendo un prefijo "w." a cada ticker
tickers_pesos_sp500 <- paste0("w.", colnames(mat.ret_sp500))
colnames(wgt_sp500) <- tickers_pesos_sp500

Finalmente, se ejecuta el algoritmo de optimización para el portafolio de mercado:

for(i in seq_along(tgt.ret_sp500)){
 # print(tgt.ret_sp500[i])
  Dmat <- 2 * (vcov_sp500 + diag(1e-6, ncol(vcov_sp500)))

  dvec <- rep(0, ncol(mat.ret_sp500))
  Amat <- cbind(rep(1, ncol(mat.ret_sp500)), avg.ret_sp500, diag(1, ncol(mat.ret_sp500)))
  bvec <- c(1, tgt.ret_sp500[i], rep(0, ncol(mat.ret_sp500)))
  sol <- quadprog::solve.QP(Dmat, dvec, Amat, bvec, meq = 2)
  
  # Guardar resultados
  tgt.sd_sp500[i] <- sqrt(sol$value)
  wgt_sp500[i, ] <- sol$solution
}

# Crear dataframe de resultados
df_sp500 <- data.frame(cbind(tgt.ret_sp500, tgt.sd_sp500, round(wgt_sp500, 8)))

Finalmente, se procederá a encontrar el portafolio de mercado de menor volatilidad:

# Encontrar portafolio de menor volatilidad
min_vol_port_sp500 <- df_sp500[which.min(df_sp500$tgt.sd_sp500), ]

O el portafolio de máximo Sharpe ratio:

# Asumiendo Rf = 0
sharpe_ratio <- df_sp500$tgt.ret_sp500 / df_sp500$tgt.sd_sp500
df_sp500$sharpe_ratio <- sharpe_ratio

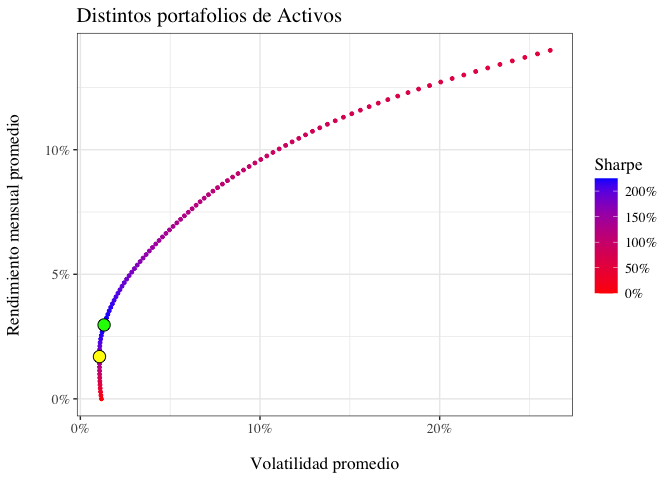
max_sharpe_port_sp500 <- df_sp500[which.max(sharpe_ratio), ]

El cual tiene un rendimiento de $2.97\%$ mensual y una volatilidad de $1.3\%$. Este portafolio se compone de los siguientes activos:

Ticker	Company	Portafolio Eficiente	Rendimiento Mensual Esperado	TEA
AVGO	Broadcom Inc.	16.76%	6.27%	107.35%
CBOE	Cboe Global Markets, Inc.	13.09%	2.28%	31.12%
NOC	Northrop Grumman Corporation	11.38%	0.33%	3.98%
XEL	Xcel Energy Inc.	10.10%	0.03%	0.38%
DELL	Dell Technologies Inc.	8.44%	4.59%	71.36%
EQT	EQT Corporation	6.72%	2.29%	31.17%
AMGN	Amgen Inc.	5.50%	0.86%	10.76%
TPL	Texas Pacific Land Corporation	5.44%	4.05%	61.03%
GOOGL	Alphabet Inc.	5.42%	2.80%	39.21%
ACGL	Arch Capital Group Ltd.	4.12%	1.68%	22.14%
META	Meta Platforms, Inc.	3.46%	6.84%	121.13%
ALL	The Allstate Corporation	2.40%	1.72%	22.68%
TYL	Tyler Technologies, Inc.	2.25%	2.71%	37.80%
ANET	Arista Networks Inc	2.08%	5.84%	97.52%
EG	Everest Group, Ltd.	1.33%	0.03%	0.36%
FOXA	Fox Corporation	0.92%	1.97%	26.38%
SMCI	Super Micro Computer, Inc.	0.59%	11.87%	284.27%

Que, gráficamente:

# Graficar la frontera eficiente
df_sp500 |>
ggplot(aes(x = tgt.sd_sp500, y = tgt.ret_sp500)) +
  geom_point(aes(color =sharpe_ratio ), size = 1) +
  geom_point(data = min_vol_port_sp500, aes(x = tgt.sd_sp500, y = tgt.ret_sp500), 
             fill = "yellow", 
             color = 'black',
             pch= 21,
             size = 4) +
  geom_point(data = max_sharpe_port_sp500, aes(x = tgt.sd_sp500, y = tgt.ret_sp500), 
             fill = "green", 
             color = 'black',
             pch= 21,
             size = 4) +
  scale_color_gradient(low = "red", high = "blue", labels = scales::percent, name = 'Sharpe') +
  scale_x_continuous(labels = scales::percent) +
  scale_y_continuous(labels = scales::percent) +
  labs(title = "Distintos portafolios de Activos", x = "\nVolatilidad promedio", y = "Rendimiento mensual promedio\n") +
  theme_bw()+
  theme(text = element_text(family = 'serif', size =13),
        )

Conclusiones

A lo largo de este documento se ha demostrado, parcialmente, el enfoque de “media-varianza” (mean-variance framework) popularizado por Harry Markowitz. Si bien ha sido un primer paso en la construcción de portafolios, se deben tener en cuenta que no está exento de críticas. Entre ellas:

Sensibilidad a las estimaciones de entrada: Los rendimientos esperados, varianzas y covarianzas se estiman a partir de datos históricos, pero pequeños errores en estas estimaciones pueden generar portafolios subóptimos.
Rendimiento distribuidos normalmente: El modelo de Markowitz supone que los rendimientos siguen una distribución normal, es decir, sin asimetría ni colas anchas. En la realidad, los rendimientos de los activos suelen presentar estas características, lo que hace que el riesgo a la baja sea mayor de lo previsto por el modelo. Entonces, la varianza no sería le mejor indicador de riesgo. Otras medidas como el VaR (Value-at-Risk) o el CVaR (Conditional VaR o Expected Shortfall) suelen preferirse sobre la varianza porque capturan mejor el riesgo de cola o downside risk.
Inconsistencia intertemporal: El modelo ignora la dinámica temporal y supone un solo período de inversión. En la inversión real, los portafolios se ajustan a lo largo del tiempo, y el riesgo cambia con el contexto de mercado. Además, como los pesos óptimos pueden cambiar significativamente ante el cambio en los insumos, de un período a otro, por ejemplo, en tres meses, el portafolio óptimo podrían cambiar considerablemente en función a los cambios en el mercado.

Finalmente, se debe tener en cuenta que la construcción de portafolios es un tema complejo y que requiere de un análisis más profundo. Por ejemplo, en el último ejercicio, el algoritmo ha seleccionado empresas del S&P 500, con crecimientos importantes, como es el caso de Super Micro Computer Inc. (SMCI) o Meta Platforms (META). Sin embargo, esto no significa que su rendimiento futuro vaya a ser similar al pasado, tomando en cuenta que pudieron haber sido grandes descubrimientos -poco usuales- los que gatillaron los precios.

Mayor información sobre esta librería, fundamental para el análisis de datos en $\mathsf{R}$, se puede encontrar en su página web, aquí. ↩︎
El ticker es un código que identifica a una acción en una bolsa de valores. Por ejemplo, el ticker de Apple es AAPL, el de Amazon es AMZN, etc. En el buscador de Yahoo Finance se pueden encontrar los tickers de las acciones que se deseen analizar. ↩︎

Última actualización el jul. 3, 2025