Gapminder

Motivación

En esta sesión se asumirá que el estudiante es la primera vez que realiza un análisis en R Markdown y, por tanto, se tendrá especial cuidado en explicar cada paso.

Librerías

R base

R cuenta con algunas librerías (conjunto de funciones) cargadas por default. Se pueden listar con el siguiente comando:

(.packages())

##  [1] "gapminder" "forcats"   "stringr"   "dplyr"     "purrr"     "readr"
##  [7] "tidyr"     "tibble"    "ggplot2"   "tidyverse" "stats"     "graphics"
## [13] "grDevices" "utils"     "datasets"  "methods"   "base"

Estos paquetes o librerías proveen a R funcionalidades básicas.

Por ejemplo, en el siguiente comando se visualizan, en orden alfabético, las primeras $10$ funciones del paquete stats:

head(ls("package:stats"),10)

##  [1] "acf"                  "acf2AR"               "add.scope"
##  [4] "add1"                 "addmargins"           "aggregate"
##  [7] "aggregate.data.frame" "aggregate.ts"         "AIC"
## [10] "alias"

Funciones bastante útiles que tomaremos de stats serán stats::median(), para obtener la mediana de un conjunto de datos, stats::cor() para calcular el coeficiente de correlación entre dos variables o stats::sd() para calcular la desviación estándar.

También se utilizarán de forma sistemática las funciones base::sum()para sumar un conjunto de datos y base::mean() para calcular su promedio

Por ejemplo:

vector <- c(4, 9, 3, 2, 2) #Creamos un vector con 5 números

base::sum(x=vector)

## [1] 20

base::mean(x=vector)

## [1] 4

stats::sd(x=vector)

## [1] 2.915476

Nótese que se ha utilizado la notación package::fun() para utilizar las funciones específicas contenidas en cada paquete o librería. ¿Por qué?

Nótese que también hubiera funcionado si hubiésemos utilizado las funciones sin referirnos a los paquetes:

vector <- c(4, 9, 3, 2, 2) #Creamos un vector con 5 números

sum(vector)

## [1] 20

mean(vector)

## [1] 4

sd(vector)

## [1] 2.915476

Como la librería ya viene cargada en R por default no es necesario indicarle desde dónde debe llamar a la función. Regularmente, las funciones que vienen en los paquetes que se abren de forma automática con el lenguaje son utilizadas directamente, sin la notación package:: previa.

Añadiendo librerías

Si bien muchas de estas funciones pueden ser útiles y están optimizadas (son rápidas), son bastante generales y quizás no sirvan para casos más específicos.

Por ejemplo, en esta sesión nos interesará entender la evolución del nivel de vida y la esperanza de vida de los países. Para tal efecto utilizaremos algunas librerías específicas. Una de ellas es gapminder.

Para instalar una librería, debemos ejecutar la función install.packages("package"), en concreto:

install.packages("gapminder")

Una vez que la librería se descarga (se requiere conexión a internet), no es necesario volverla a instalarla puesto que ya se encuentra en un archivo en nuestra PC ¹.

Ahora, para poder utilizar las funciones propias de la librería, en este caso de gapminder, se pueden tomar tres caminos:

1. Cargar la librería entera (todas las funciones) utilizando la sintaxis `library("package")`,
1. Cargar las funciones conforme se vayan necesitando, utilizando la sintaxis `package::fun()`,
1. Una mezcla de ambas.

En este caso, para fines pedagógicos, se utilizará el 3er. punto:

library(gapminder)

Y, una vez cargada, las funciones que contiene, por orden alfabético, son:

ls("package:gapminder")

## [1] "continent_colors"     "country_codes"        "country_colors"
## [4] "gapminder"            "gapminder_unfiltered"

En particular, la que nos interesará es gapminder::gapminder, pues contiene el conjunto de datos que se se utilizará:

Utilizaremos también otras funciones, más especializadas, contenidas en los siguientes paquetes:

install.packages("readr") #Funciones para leer documentos
install.packages("dplyr") #Funciones para limpiar, transformar y agregar datos
install.packages("ggplot2") #Funciones para visualizar datos
install.packages("magrittr") #Paquete que contiene el operador pipe, %>%.
install.packages("tidyr") #Funciones convenientes para pasar de formato ancho a formato largo y viceversa

install.packages("tidyverse")

Y, las cargamos:

library(readr)
library(dplyr)
library(ggplot2)
library(magrittr)
library(tidyr)

# library(tidyverse)

Cargando los datos

Una vez tenemos las librerías listas para nuestro análisis, el primer paso para realizar un análisis (econométrico) es el cargado de la información.

En este caso concreto, como ya se mencionó, los datos se encuentran en la librería gapminder:

data <- gapminder::gapminder #Cargar los datos

Con los datos cargados², comenzamos entendiendo la información que contiene.

Una primera aproximación es utilizar la interfaz de RStudio para visualizar los datos y entender la estructura de los mismos. Esto se puede realizar haciendo click sobre el objeto data que acabamos de crear. De forma equivalente, se puede escribir en el prompt View(data) y se abrirá una nueva ventana.

En nuestro caso, se visualizarán las primeras $20$ filas para tener una pequeña idea de lo que contiene el conjunto de datos:

head(data, 20)

## # A tibble: 20 x 6
##    country     continent  year lifeExp      pop gdpPercap
##    <fct>       <fct>     <int>   <dbl>    <int>     <dbl>
##  1 Afghanistan Asia       1952    28.8  8425333      779.
##  2 Afghanistan Asia       1957    30.3  9240934      821.
##  3 Afghanistan Asia       1962    32.0 10267083      853.
##  4 Afghanistan Asia       1967    34.0 11537966      836.
##  5 Afghanistan Asia       1972    36.1 13079460      740.
##  6 Afghanistan Asia       1977    38.4 14880372      786.
##  7 Afghanistan Asia       1982    39.9 12881816      978.
##  8 Afghanistan Asia       1987    40.8 13867957      852.
##  9 Afghanistan Asia       1992    41.7 16317921      649.
## 10 Afghanistan Asia       1997    41.8 22227415      635.
## 11 Afghanistan Asia       2002    42.1 25268405      727.
## 12 Afghanistan Asia       2007    43.8 31889923      975.
## 13 Albania     Europe     1952    55.2  1282697     1601.
## 14 Albania     Europe     1957    59.3  1476505     1942.
## 15 Albania     Europe     1962    64.8  1728137     2313.
## 16 Albania     Europe     1967    66.2  1984060     2760.
## 17 Albania     Europe     1972    67.7  2263554     3313.
## 18 Albania     Europe     1977    68.9  2509048     3533.
## 19 Albania     Europe     1982    70.4  2780097     3631.
## 20 Albania     Europe     1987    72    3075321     3739.

Adicionalmente, para saber qué tipo de análisis se aplicará, es importante conocer el tipo de datos de los que disponemos:

str(data)

## tibble [1,704 x 6] (S3: tbl_df/tbl/data.frame)
##  $ country  : Factor w/ 142 levels "Afghanistan",..: 1 1 1 1 1 1 1 1 1 1 ...
##  $ continent: Factor w/ 5 levels "Africa","Americas",..: 3 3 3 3 3 3 3 3 3 3 ...
##  $ year     : int [1:1704] 1952 1957 1962 1967 1972 1977 1982 1987 1992 1997 ...
##  $ lifeExp  : num [1:1704] 28.8 30.3 32 34 36.1 ...
##  $ pop      : int [1:1704] 8425333 9240934 10267083 11537966 13079460 14880372 12881816 13867957 16317921 22227415 ...
##  $ gdpPercap: num [1:1704] 779 821 853 836 740 ...

De lo anterior, vemos que este dataset contiene $1706$ filas y $6$ columnas que contienen datos de la esperanza de vida, $lifeExp$, población, $pop$ y PIB per cápita, $gdpPercap$ para $142$ países en distintos años.

Nótese que las distintas columnas o características tienen distintos tipos: $country$ y $continent$ son factores o Factor, $year$ y $pop$ son números enteros o int y, finalmente, $lifeExp$ y $gdpPercap$ son datos numéricos o num. Aunque ahora podemos avanzar sin perder generalidad, más adelante será importante distinguir sobre estos tipos pues, distintas funciones (o métodos), solo aplican para tipos determinados. Por ejemplo, la función base::sum() se comportará distinto cuando le pasemos como argumento un dato de tipo num que cuando le pasemos otro de tipo Factor.

Transformación y Agregación

Pasos previos

En esta sección vamos a utilizar mayormente las funciones contenidas en la librería dplyr, pues proveen una sintaxis consistente para transformar y agregar los datos de forma rápida y entendible.

Entre estas funciones, se pueden encontrar:

set.seed(12)
sample(ls("package:dplyr"),20)

##  [1] "storms"                "nest_by"               "db_drop_table"
##  [4] "changes"               "group_vars"            "dplyr_reconstruct"
##  [7] "distinct"              "group_by_drop_default" "filter_all"
## [10] "filter"                "semi_join"             "tbl_ptype"
## [13] "last"                  "db_insert_into"        "group_indices_"
## [16] "with_order"            "explain"               "bind_cols"
## [19] "sql_subquery"          "ungroup"

Ahora, se podría argumentar que esta etapa es una de descubrimiento. Es un proceso de data discovery o, como le llaman en el campo del análisis de datos o data science es parte del Exploratory Data Analysis (EDA).

En este punto el investigador o analista puede o:

1. No tener ninguna idea sobre lo que contiene el conjunto de datos o
2. Estar buscando algo específico

En el primer caso, habrá que familiarizarse con todo el conjunto de datos primero y, más importante, con el proceso que generó la información o Data Generating Process (DGP) para intuir la historia (ojalá causal) que originó los datos que se tiene.

En el segundo caso, ya se cuenta con una pregunta específica que se tratará de responder utilizando la información disponible.

En ambos casos, el investigador debe estar abierto a entender la información que se presenta, antes de forzar la misma a las conclusiones o ideas que se tienen ex ante el análisis de información. A partir de los datos, entonces, vamos a poder afinar nuestra idea inicial sobre esta realidad.

Analizando la información

Algunas preguntas que pueden ser interesantes de responder son:

1. ¿Cómo ha evolucionado la esperanza de vida y el PIB per cápita en el mundo a lo largo del tiempo? ¿Estamos mejor ahora que al comienzo del período?
1. ¿Qué continente tiene un mejor nivel de vida?
1. ¿Cuál es el país que tenía mayor esperanza de vida y PIB per cápita en el primer período y cuál lo es ahora?
1. ¿Cuáles son los países con mayor incremento poblacional?

Nótese dos cosas: 1. Las respuestas a estas preguntas (y a muchas otras) están contenidas en los datos pero no son evidentes a partir de los datos en bruto, es decir, se requiere hacer alguna transformación o extraer solamente la información útil para responder cada pregunta y 2. El tipo de preguntas que se ha realizado son preguntas descriptivas, en el sentido que pueden responderse mirando correctamente a la información. Esto contrasta con los tipos de preguntas causales que son el interés principal del curso. Sin embargo, entender los datos (describirlos) es siempre un buen comienzo.

Evolución de la esperanza de vida y el PIB per cápita

En este sentido, como se tienen muchos países y muchos períodos, lo que se necesita es una forma de agregarlos. Por ejemplo, podríamos calcular tanto la esperanza de vida como el PIB per cápita promedio de todos los países para cada año:

prom_mundial <- data |>
    dplyr::group_by(year) |>
    dplyr::summarise(PIBpercap_prom = mean(gdpPercap),
                     Esp_prom = mean(lifeExp))

prom_mundial

## # A tibble: 12 x 3
##     year PIBpercap_prom Esp_prom
##    <int>          <dbl>    <dbl>
##  1  1952          3725.     49.1
##  2  1957          4299.     51.5
##  3  1962          4726.     53.6
##  4  1967          5484.     55.7
##  5  1972          6770.     57.6
##  6  1977          7313.     59.6
##  7  1982          7519.     61.5
##  8  1987          7901.     63.2
##  9  1992          8159.     64.2
## 10  1997          9090.     65.0
## 11  2002          9918.     65.7
## 12  2007         11680.     67.0

Nótese los resultados. Se observa que el PIB per cápita mundial ha ido creciendo desde USD $3725.276$ en $1952$ hasta USD $11680.072$ el $2007$³. Con la esperanza de vida sucede algo similar.

Ahora, alguien podría razonar y argumentar que, en vez de usar el promedio simple por país, sería mejor utilizar un promedio ponderado por la cantidad de habitantes de cada país. Esto para reflejar mejor el hecho de que un país con una población muy grande pero rica y saludable, podría estar valiendo lo mismo que un país pequeño pero de escaso recursos y poco saludable.

Para arreglar por esto, corregimos nuestro código:

prom_mundial_w <- data %>%
    dplyr::group_by(year)%>%
    dplyr::summarise(PIBpercap_prom = weighted.mean(gdpPercap,w=pop),
                     Esp_prom = weighted.mean(lifeExp,w=pop))

prom_mundial_w

## # A tibble: 12 x 3
##     year PIBpercap_prom Esp_prom
##    <int>          <dbl>    <dbl>
##  1  1952          2924.     48.9
##  2  1957          3339.     52.1
##  3  1962          3795.     52.3
##  4  1967          4428.     57.0
##  5  1972          5150.     59.5
##  6  1977          5679.     61.2
##  7  1982          5917.     62.9
##  8  1987          6423.     64.4
##  9  1992          6751.     65.6
## 10  1997          7435.     66.8
## 11  2002          8029.     67.8
## 12  2007          9296.     68.9

Nótese que, corrigiendo por la cantidad de habitantes, los resultados difieren. Por ejemplo, en $1952$ el PIB per cápita mundial fue de $2923.895$ y en el $2007$ mejoró llegando a $9295.987$. En ambos casos, el PIB per cápita obtenido utilizando un promedio ponderado fue menor al obtenido utilizando promedios simples. ¿Por qué?

Continentes y nivel de vida

En este caso, asumiendo que el nivel de vida se obtiene o por producir (y vender más), es decir, teniendo un PIB per cápita más grande o por vivir más tiempo, teniendo una mejor esperanza de vida, se puede responder la pregunta agregando la información:

vida_x_cont <- data %>%
    group_by(continent)%>%
    summarise(PIBpercap_prom = mean(gdpPercap),
              Esp_prom = mean(lifeExp),
              PIBpercap_promp = weighted.mean(gdpPercap,pop),
              Esp_promp = weighted.mean(lifeExp,pop))
vida_x_cont

## # A tibble: 5 x 5
##   continent PIBpercap_prom Esp_prom PIBpercap_promp Esp_promp
##   <fct>              <dbl>    <dbl>           <dbl>     <dbl>
## 1 Africa             2194.     48.9           2108.      50.6
## 2 Americas           7136.     64.7          15477.      69.5
## 3 Asia               7902.     60.1           2950.      61.1
## 4 Europe            14469.     71.9          15693.      72.3
## 5 Oceania           18622.     74.3          21205.      75.5

¿Está bien este resultado? La respuesta es que no. El problema es que estamos tomando el promedio simple de los continente independientemente de los años. Corrigiendo:

vida_x_cont_x_periodo <- data %>%
    group_by(year,continent)%>%
    summarise(PIBpercap_prom = mean(gdpPercap),
              Esp_prom = mean(lifeExp),
              PIBpercap_promp = weighted.mean(gdpPercap,pop),
              Esp_promp = weighted.mean(lifeExp,pop))
vida_x_cont_x_periodo

## # A tibble: 60 x 6
## # Groups:   year [12]
##     year continent PIBpercap_prom Esp_prom PIBpercap_promp Esp_promp
##    <int> <fct>              <dbl>    <dbl>           <dbl>     <dbl>
##  1  1952 Africa             1253.     39.1           1311.      38.8
##  2  1952 Americas           4079.     53.3           8528.      60.2
##  3  1952 Asia               5195.     46.3            806.      42.9
##  4  1952 Europe             5661.     64.4           6097.      64.9
##  5  1952 Oceania           10298.     69.3          10136.      69.2
##  6  1957 Africa             1385.     41.3           1445.      40.9
##  7  1957 Americas           4616.     56.0           9098.      62.0
##  8  1957 Asia               5788.     49.3            998.      47.3
##  9  1957 Europe             6963.     66.7           7535.      66.9
## 10  1957 Oceania           11599.     70.3          11192.      70.3
## # ... with 50 more rows

La respuesta está, sin duda en esta agregación aunque es difícil de leerla en forma tabular. Quizás la comparación es más sencilla si filtramos el último año, que es el que nos interesa. Para esto podemos utilizar dplyr::filter()

vida_x_cont_x_periodo %>%
    #filter(year==2007)
    filter(continent == "Asia",year %in% c(1952,2007))

## # A tibble: 2 x 6
## # Groups:   year [2]
##    year continent PIBpercap_prom Esp_prom PIBpercap_promp Esp_promp
##   <int> <fct>              <dbl>    <dbl>           <dbl>     <dbl>
## 1  1952 Asia               5195.     46.3            806.      42.9
## 2  2007 Asia              12473.     70.7           5432.      69.4

Tomando en cuenta los promedios ponderados, Oceanía es el continente que disfruta de una mejor calidad de vida, ya sea comparando por PIB per cápita o por esperanza de vida.

Cambios demográficos

Este conjunto de datos, también almacena la cantidad de habitantes,$pop$, que tenía cada país en distintos años, comenzando por $1952$.

Por tanto, sería interesante ver qué país ha incrementado más su población. En este sentido comparando el primer año de los datos con el último podría ser suficiente. Esto lo expresaremos de forma porcentual:

cambio_dem = data %>%
    filter(year %in% c(1952, 2007))%>%
    group_by(country)%>%
    summarise(cambio_pop_abs = diff(pop,L=1),
              cambio_pop_rel = cambio_pop_abs*100/lag(pop))%>%
    filter(!is.na(cambio_pop_rel))%>%
    arrange(desc(cambio_pop_rel))
cambio_dem

## # A tibble: 142 x 3
## # Groups:   country [142]
##    country       cambio_pop_abs cambio_pop_rel
##    <fct>                  <int>          <dbl>
##  1 Kuwait               2345559          1466.
##  2 Jordan               5445279           896.
##  3 Djibouti              433225           686.
##  4 Saudi Arabia        23595361           589.
##  5 Oman                 2697064           531.
##  6 Cote d'Ivoire       15036390           505.
##  7 Gambia               1404039           494.
##  8 Libya                5017185           492.
##  9 Bahrain               588126           488.
## 10 Kenya               29146131           451.
## # ... with 132 more rows

De esta tabla se deriva que Kuwait, Jordan, Djibouti, Saudi Arabia y Oman han sido los países que más han crecido en términos relativos entre $1952$ y el $2007$.

Visualización

The basics

Ahora, se dice que una imagen vale más que mil palabras. En esta sección se ilustrarán algunas visualizaciones simple utilizando la librería ggplot2⁴.

Esta librería lleva su nombre a partir de grammar of graphics (por eso, “gg”) y básicamente es una sintaxis para crear visualizaciones. En concreto, esta sintaxis funciona por capas (o “layers”) que van agregando geometrías al gráfico. Se puede pensar esto como colocando un lienzo en blanco y luego se va construyendo por partes: se pinta un marco, se pinta el fondo, luego se pintan a los personajes del cuadro, luego se agregan colores, etc.

Por ejemplo, para crear el lienzo en blanco solo se llama a la función ggplot2::ggplot()

ggplot2::ggplot()

Como se ve, es un cuadro en blanco. Vamos a crear un dataframe con algunos puntos aleatorios para graficarlos.

set.seed(123)
df_ggplot <- data.frame(var_x= c(1:10), var_y = runif(10, min=0, max=10))
df_ggplot$var_z <- ifelse(df_ggplot$var_y>5, yes="Mayor a 5", no="Menor a 5")

df_ggplot

##    var_x    var_y     var_z
## 1      1 2.875775 Menor a 5
## 2      2 7.883051 Mayor a 5
## 3      3 4.089769 Menor a 5
## 4      4 8.830174 Mayor a 5
## 5      5 9.404673 Mayor a 5
## 6      6 0.455565 Menor a 5
## 7      7 5.281055 Mayor a 5
## 8      8 8.924190 Mayor a 5
## 9      9 5.514350 Mayor a 5
## 10    10 4.566147 Menor a 5

Entonces, se añadirá la geometría de puntos al lienzo inicial:

df_ggplot %>%
    ggplot(aes(x=var_x, y=var_y))+
    geom_point()

Como se observa en el gráfico precedente, se han graficado los puntos. Nótese, sin embargo, que dentro de la función ggplot2::ggplot() se ha añadido la función aes(). Esta función se conoce como el “aesthetic” o “estéticos” del gráfico y básicamente es la información o datos que se quiere visualizar. Se debe indicar que cada capa o geometría puede tener sus propios aes() pero cuando se lo especifica dentro de ggplot2::ggplot() todas las siguientes geometrías “heredan” los mismos aes(). En gráficos simples como los que se verán aquí no habrá problema en especificar aes() al inicio.

df_ggplot %>%
    ggplot()+
    geom_point(aes(x=var_x, y=var_y))

Existen distintas argumentos para aes() y es posible controlar casi todos los detalles del gráficos: colores, tamaños, añadir texto, etc⁵. Por ejemplo, podríamos añadir “color” a los puntos en función a una tercer variable:

df_ggplot %>%
    ggplot(aes(x=var_x, y=var_y, color=var_z))+
    geom_point(size= 3)

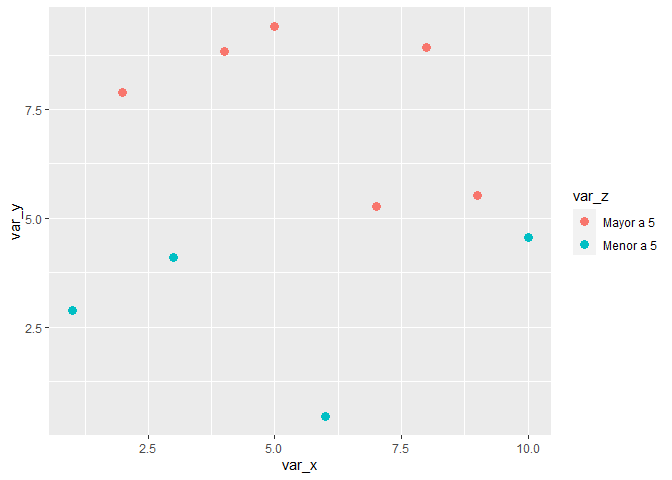
Finalmente, se pueden añadir más estéticos y geometrías para tener una imagen un poco mejor acabada:

df_ggplot %>%
    ggplot(aes(x=var_x, y=var_y, fill=var_z))+
    geom_point(color="black", shape=21, size= 3)+
    labs(title="Puntos generados aleatoriamente para ilustrar cómo funciona ggplot2",
         x="\nVariable X", y="Variable Y\n" )+
    scale_fill_manual("¿Mayor a 5?", values = c("green", "gray"))+
    geom_hline(yintercept = 5, color="red", linetype="dashed")+
    theme_bw()

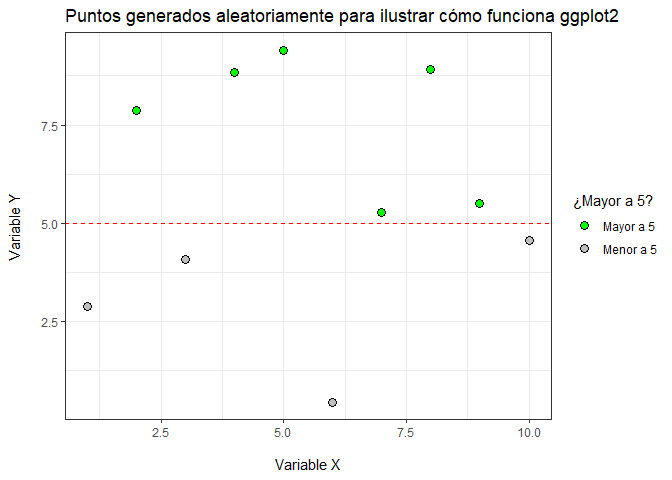
Así, ggplot2 provee de una sintaxis conveniente y lo suficientemente flexible como para desplegar todo tipo de información⁶.

The Gapminder

Volviendo al ejemplo, sería interesante responder las preguntas abordadas de formar numérica pero esta vez matizadas de forma gráfica. Por conveniencia, se reproducen nuevamente las preguntas:

1. ¿Cómo ha evolucionado la esperanza de vida y el PIB per cápita en el mundo a lo largo del tiempo? ¿Estamos mejor ahora que al comienzo del período?
1. ¿Qué continente tiene un mejor nivel de vida?
1. ¿Cuál es el país que tenía mayor esperanza de vida y PIB per cápita en el primer período y cuál lo es ahora?
1. ¿Cuáles son los países con mayor incremento poblacional?

Antes de proceder, nos aseguramos de tener los datos cargados:

data <- gapminder::gapminder #Cargar los datos

Evolución en el tiempo

Para graficar la evolución en el tiempo, se utilizarán algunos objetos que ya han sido creados anteriormente con algunas ligeras modificaciones para poder “pasarlos” a ggplot2.

Adicionalmente, se procederá en dos etapas por razones pedagógicas, aunque no es estrictamente necesario. En la primera se creará el objeto que se desea visualizar (tabla con información) y en la segunda parte se procederá a crear su gráfico respectivo.

prom_mundial <- data |>
    dplyr::group_by(year) |>
    dplyr::summarise(PIBpercap_prom = mean(gdpPercap),
                     Esp_prom = mean(lifeExp))

prom_mundial

## # A tibble: 12 x 3
##     year PIBpercap_prom Esp_prom
##    <int>          <dbl>    <dbl>
##  1  1952          3725.     49.1
##  2  1957          4299.     51.5
##  3  1962          4726.     53.6
##  4  1967          5484.     55.7
##  5  1972          6770.     57.6
##  6  1977          7313.     59.6
##  7  1982          7519.     61.5
##  8  1987          7901.     63.2
##  9  1992          8159.     64.2
## 10  1997          9090.     65.0
## 11  2002          9918.     65.7
## 12  2007         11680.     67.0

Existe una particularidad adicional con lo que se va a realizar a continuación. Hay una diferencia técnica entre formatos tabulares “largos” y formatos tabulares “cortos”. Aunque esto escapa del alcance del curso, se debe puntualizar que, para graficar series temporales ggplot2 prefiere estructura de datos “largas”. Para conseguir esto se utilizará tidyr::pivot_longer, a continuación:

prom_mundial_long <- data %>%
    dplyr::group_by(year) %>%
    dplyr::summarise(PIBpercap_prom = weighted.mean(gdpPercap,pop),
                     Esp_prom = weighted.mean(lifeExp,pop)) %>%
    tidyr::pivot_longer(!year, names_to="Variable",values_to="Valor")

prom_mundial_long$Variable <- factor(prom_mundial_long$Variable, levels = c("Esp_prom","PIBpercap_prom"),
                                     labels=c("Esperanza de Vida al Nacer (promedio ponderado)", "PIB per cápita (promedio ponderado)"))

prom_mundial_long

## # A tibble: 24 x 3
##     year Variable                                         Valor
##    <int> <fct>                                            <dbl>
##  1  1952 PIB per cápita (promedio ponderado)             2924.
##  2  1952 Esperanza de Vida al Nacer (promedio ponderado)   48.9
##  3  1957 PIB per cápita (promedio ponderado)             3339.
##  4  1957 Esperanza de Vida al Nacer (promedio ponderado)   52.1
##  5  1962 PIB per cápita (promedio ponderado)             3795.
##  6  1962 Esperanza de Vida al Nacer (promedio ponderado)   52.3
##  7  1967 PIB per cápita (promedio ponderado)             4428.
##  8  1967 Esperanza de Vida al Nacer (promedio ponderado)   57.0
##  9  1972 PIB per cápita (promedio ponderado)             5150.
## 10  1972 Esperanza de Vida al Nacer (promedio ponderado)   59.5
## # ... with 14 more rows

Nótese de la tabla anterior, que se ha “alargado” la tabla. Es decir, en vez de tener una columna tanto para el PIB per cápita como para la Esperanza de Vida, se tiene solamente una. La forma “ancha” de la tabla anterior tendría la siguiente forma:

year	PIB per cápita	Esperanza de Vida
1952	2923.89	48.94
1957	3338.93	52.12
1962	3794.89	52.32
1967	4428.34	56.98

prom_mundial_long %>%
    ggplot(aes(x=year, y=Valor))+
    geom_line(size=1.1,color="blue")+
    facet_wrap(~Variable,
               scales="free_y")+
    geom_smooth(method='lm', formula= y~x, se=FALSE, color="red", linetype="dashed", size=0.75)+
    theme_bw()

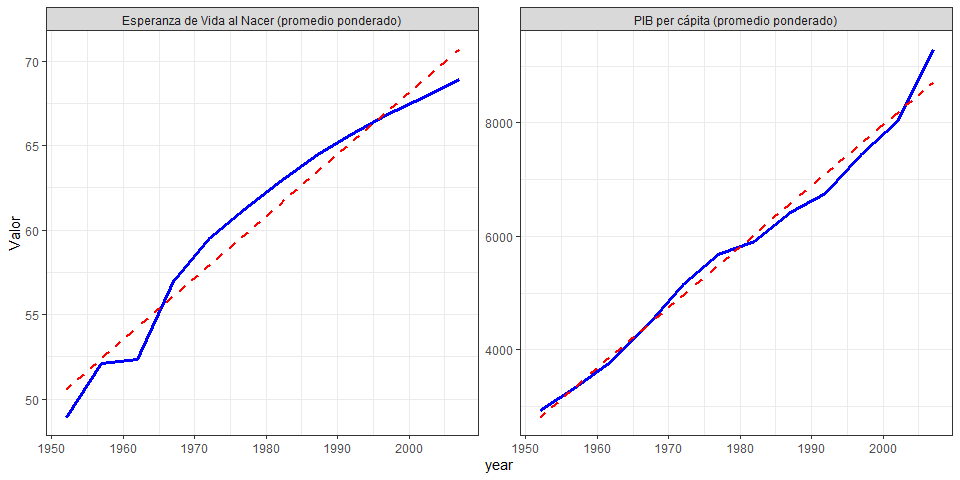
¿Qué se observa? Las líneas azules son los niveles tanto de la Esperanza de Vidal al Nacer como del PIB per cápita, ponderados por la cantidad de población que tiene cada país. En el caso del primero, se observa un quiebre entre $1957$ y $1962$ y luego un crecimiento sostenido pero a tasas decrecientes. En el caso del segundo, se registra un cambio de tendencia en $1967$.

Las líneas rojas segmentadas se pueden entender como una especie de tendencia: Si la línea azul está por encima significaría que se está creciendo más rápido de lo que se hubiera predicho.

Se puede responder, por tanto, que estamos mucho mejor ahora (en $2007$, para ser exactos) que lo que estábamos en $1952$ tomando en cuenta solamente estos indicadores.

Continente con mejor nivel de vida

En cuanto al análisis por continente, se puede representar gráficamente, para cada indicador, los niveles tanto en $1952$ como en $2007$:

 cambio_continente <- data %>%
    filter(year %in% c(1952,2007))%>%
    group_by(year,continent)%>%
    summarise(PIBpercap_promp = weighted.mean(gdpPercap,pop),
              Esp_promp = weighted.mean(lifeExp,pop),.groups = "drop_last")%>%
    tidyr::pivot_longer(!c(year,continent), names_to="Variable",values_to="Valor")

cambio_continente$Variable = factor(cambio_continente$Variable, levels = c("Esp_promp","PIBpercap_promp"),
                                     labels=c("Esperanza de Vida al Nacer (promedio ponderado)", "PIB per cápita (promedio ponderado)"))

cambio_continente %>%
    ggplot(aes(x=reorder(continent,-Valor,weighted.mean), y=Valor,fill=factor(year)))+
    geom_bar(color="black",stat="identity", position = "dodge")+
    facet_wrap(~Variable, scale="free_y")+
    labs(title = "Cambio en la Esperanza de Vida y PIB per cápita entre 1952 y 2007",
         x="\nContinentes", y="Valor \n")+
    scale_fill_manual("Año",values = c("gray","green"))+
    theme_bw()

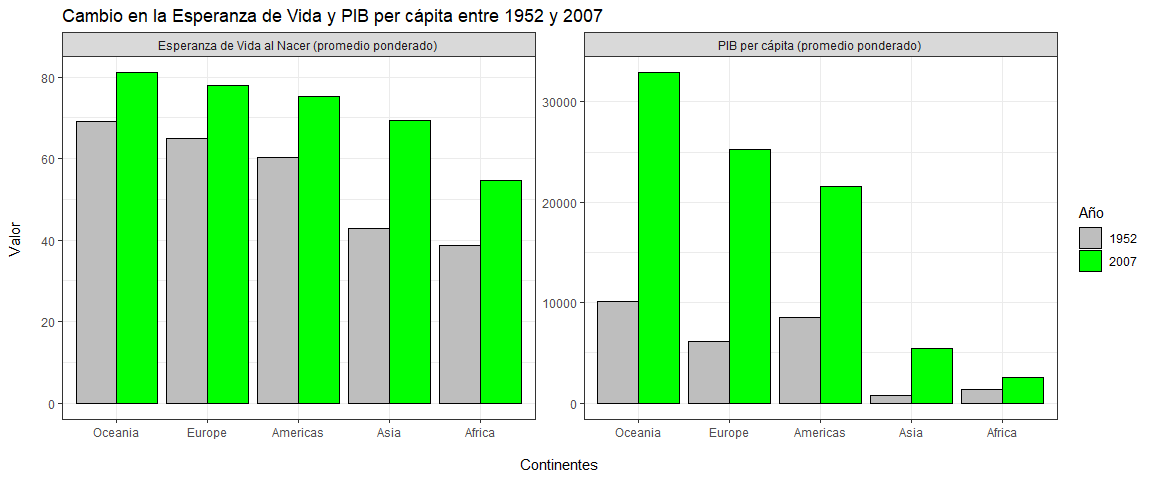
Se observa que en $1952$ (barras grises) era Oceanía el que tenía una mayor esperanza de vida (alrededor de los $70$ años), mientras que África era el peor (alrededor de los $40$ años). En el caso del PIB el patrón se repite.

Lo que resulta interesante es que, al $2007$, se observa el mismo patrón (Oceanía primero, África último) pero, se observa saltos “más grandes” de los continente africanos y asiáticos, al menos en esperanza de vida.

Diferencias entre países

Finalmente, es esta sección se ilustrarán los países que más y menos han incrementado su población en el período de tiempo estudiado.

Inicialmente, se encuentra el cambio porcentual entre los valores de de $1952$ y $2007$ para ordenar a los países de mayor a menor. Posteriormente se tomarán los $9$ primeros y los $9$ últimos.

En el caso del top $9$ tenemos:

cambio_dem_viz = data %>%
    filter(year %in% c(1952, 2007))%>%
    group_by(country)%>%
    summarise(cambio_pop_rel = diff(pop,L=1)*100/lag(pop),.groups = "drop_last")%>%
    filter(!is.na(cambio_pop_rel))%>%
    arrange(desc(cambio_pop_rel))

top <- cambio_dem_viz[c(1:9),"country"]

data %>%
    filter(country %in% top$country) %>%
    select(country,year, pop) %>%
    ggplot(aes(x=year, y= pop/1000000))+
    geom_line(size=1, color="blue")+
    facet_wrap(~factor(country,levels=c(top$country)),scales = "free_y")+
    labs(title = "Países con mayor crecimento poblacional entre 1952 y 2007",
         x="\nAño",y="Población (en millones de habitantes)\n")+
    geom_smooth(method='lm', formula= y~x, se=FALSE, color="red", linetype="dashed", size=0.75)+
    theme_bw()

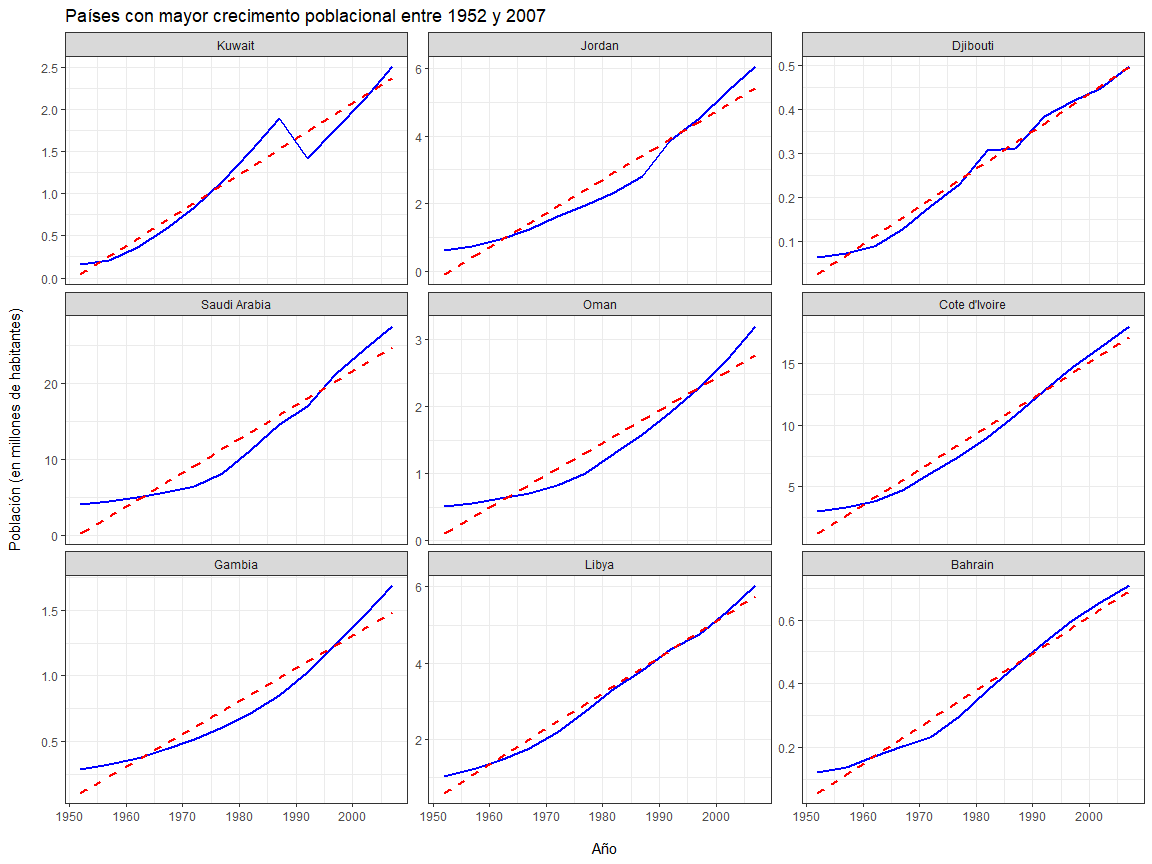
Donde se observa que Kuwait, Jordan y Djibouti son los países que más han crecido en términos relativos. Nótese que a partir de esta información (hechos) no se puede explicar el porqué. Conocedores de la historia moderna de Kuwait, por ejemplo, podrán argumentar sobre posibles factores que han afectado o incidido en este crecimiento, sin embargo, no será definitivo para establecer todas las “causas” y su contribución a este crecimiento.

En el caso de los países que han crecido menos tenemos:

cambio_dem_viz_min = data %>%
    filter(year %in% c(1952, 2007))%>%
    group_by(country)%>%
    summarise(cambio_pop_rel = diff(pop,L=1)*100/lag(pop),.groups="drop_last")%>%
    filter(!is.na(cambio_pop_rel))%>%
    arrange(cambio_pop_rel)

bottom <- cambio_dem_viz_min[c(1:9),"country"]

data %>%
    filter(country %in% bottom$country) %>%
    select(country,year, pop) %>%
    ggplot(aes(x=year, y= pop/1000000))+
    geom_line(size=1, color="blue")+
    facet_wrap(~factor(country,levels = bottom$country),scales = "free_y")+
    labs(title = "Países con menor crecimento poblacional entre 1952 y 2007",
         x="\nAño",y="Población (en millones de habitantes)\n")+
    geom_smooth(method='lm', formula= y~x, se=FALSE, color="red", linetype="dashed", size=0.75)+
    theme_bw()

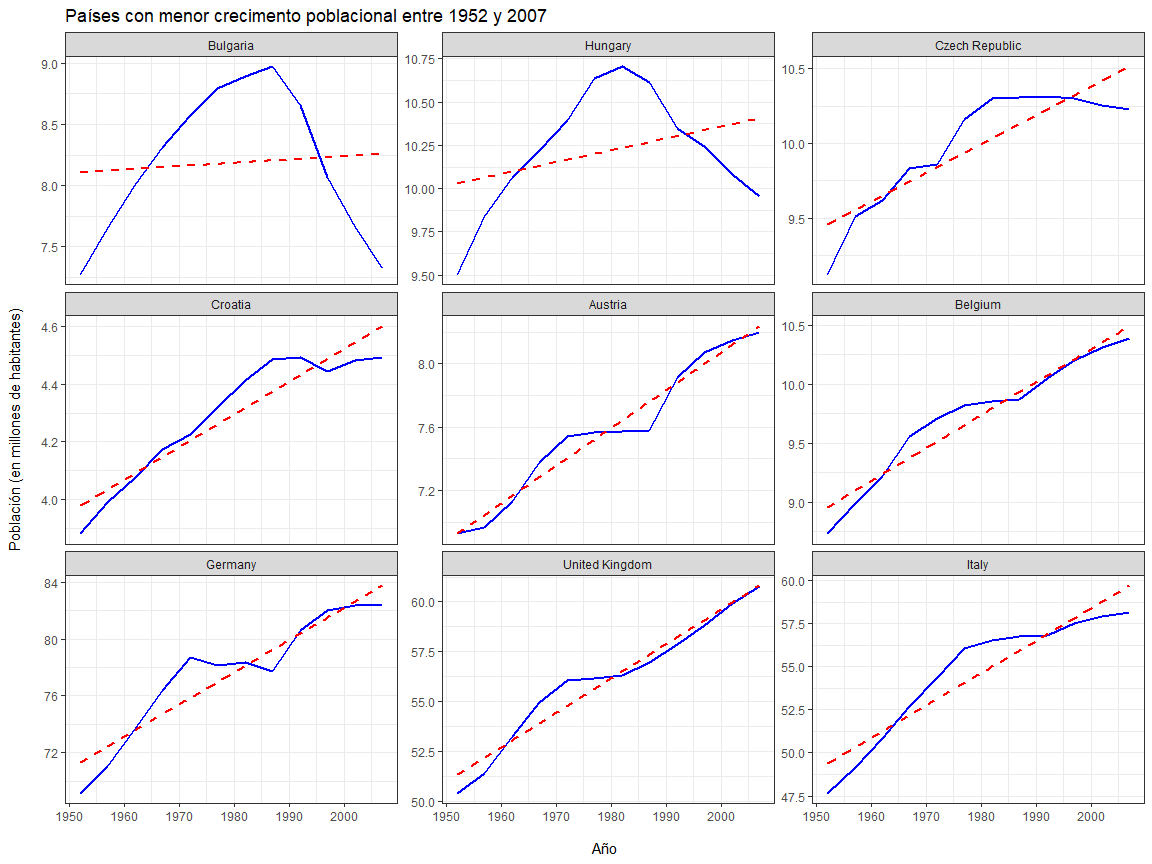
Se observa que Bulgaria, Hungría y República Checa son los países que menos han crecido en el periodo de $55$ años que comprenden nuestros datos.

Al igual que se observó en el gráfico anterior (el top 9), no tenemos suficiente información para explicar o entender porqué, por ejemplo, la población de Bulgaria crece hasta la década del $90$ y luego cae precipitadamente. Una búsqueda rápida en internet da cuenta de este hecho e indica, por ejemplo, que los jóvenes se están yendo del país en búsqueda de trabajos más lucrativos⁷.

Conclusiones

En este documento se ha tratado de mostrar el proceso general de análisis de datos, en particular, utilizando la herramienta R Markdown. Este proceso comprende la gestión de librerías y pasos previos en nuestra herramienta, el cargado de la información, la transformación y agregación de datos, la visualización y, aunque no se ha cubierto en esta parte, el análisis de los resultados.
Existen varias formas de cargar los datos a RStudio: desde una base de datos, desde nuestra computadora, desde una url, etc. También, R puede leer un sinnúmero de formatos: .txt, .csv, .xlsx, etc.
Aunque difícil de entender inicialmente, R y RStudio son herramientas valiosas para mejorar la capacidad de análisis, automatizar tareas rutinarias y, finalmente, mejorar la productividad en las tareas de análisis y publicación de información.

Nótese que en este ejemplo específico se ha colocado eval= FALSE en la cabecera del código (del chunk) para evitar que la instalación se ejecute cada vez que se exporta el R Markdown a otro formato. ↩︎
Otra forma de cargar la información desde fuera, en concreto, desde un archivo Excel con extensión .csv (comma separated values) es utilizar readr::read_csv(file= ".\path\archive.csv". Para más información, colocar en el prompt ?readr::read_csv. ↩︎
Desde el punto de vista económico, para que éstas comparaciones tengan sentido debe utilizarse el PIB per cápita real, esto es, desprovisto de las unidades de medida monetarias. Adicionalmente deben ajustarse los datos por el poder adquisitivo que tiene una suma de dinero determinada en cada país (países más pobres tienen también precios más bajos) y deben realizarse algunos ajustes por tipos de cambio, etc. Una tabla que permite realizar este tipo de comparaciones es la Penn World Table. ↩︎
Para aprender los detalles y matices de ggplot2 ingresar a su página principal aquí. ↩︎
En rigor, hay un sinnúmero de estéticos y geometrías. Un documento que condensa esa información es el cheatsheet que ha elaborado el equipo de RStudio y que se puede descargar haciendo click aquí. ↩︎
Un buen lugar para obtener inspiración (y los códigos fuente) es The R Graph Gallery donde se encuentran ejemplos con distintas geometrías y distintos tipos de datos. ↩︎
Puede ver el detalle en este post del Washington Post del 7 de enero de 2022. ↩︎

Última actualización el May 5, 2018